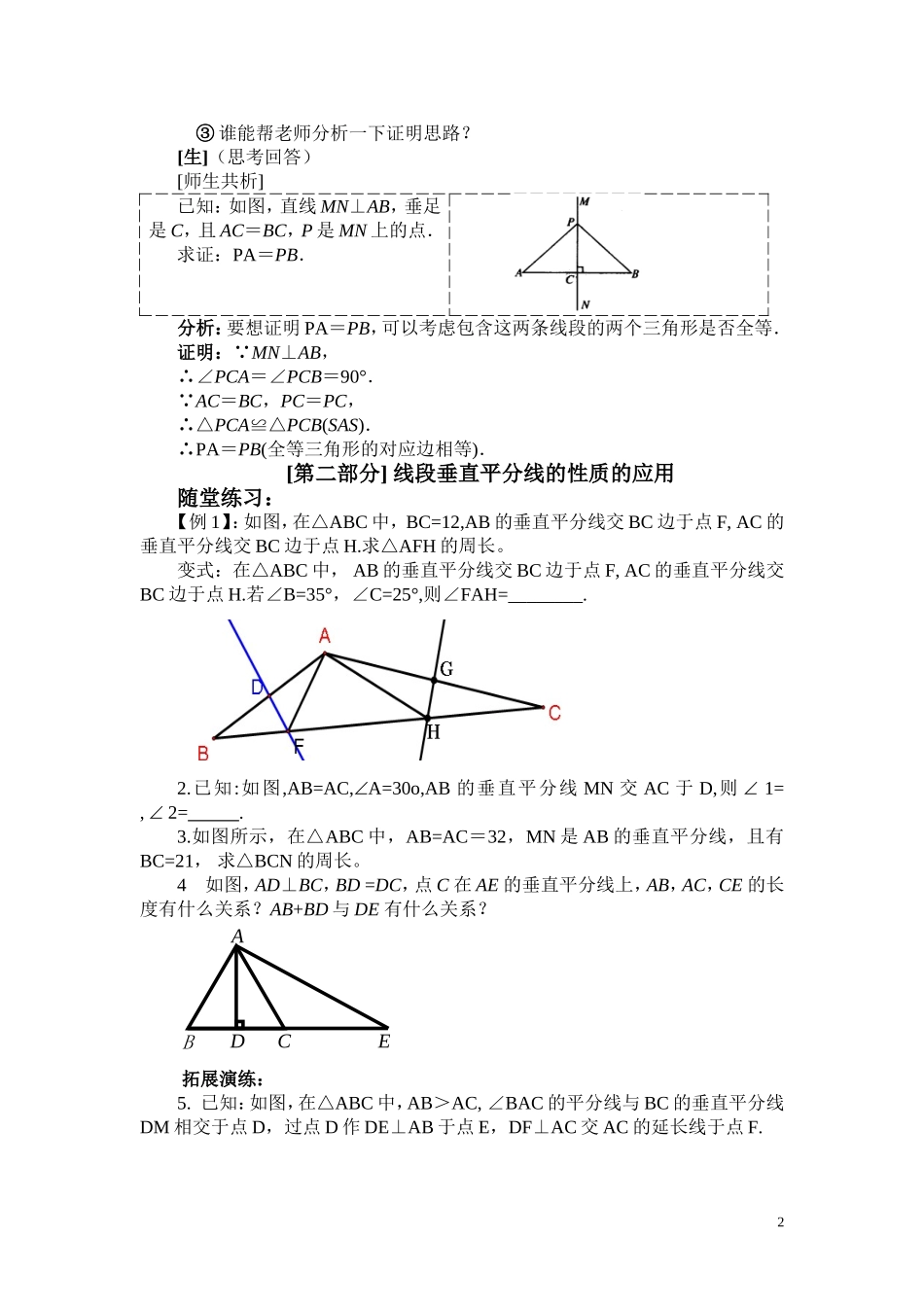
§1.3.1线段的垂直平分线的性质(教案)——卫艳艳教学目标1.经历探索、猜测过程,能够运用公理和所学过的定理证明线段垂直平分线的性质定理.2.经历探索、猜测、证明的过程,进一步发展学生的推理证明意识和能力.3.体验解决问题策略的多样性,发展实践能力和创新精神.教学重点1.能够证明线段的垂直平分线的性质定理.2.能够利用尺规作已知线段的垂直平分线.教学难点线段垂直平分线的性质教学方法与手段:采用“情境──探究”的方法教学过程Ⅰ.创设现实情境,引入新课教师用多媒体演示:如图,A、B表示两个仓库,要在A、B一侧的河岸边建造一个码头,使它到两个仓库的距离相等,码头应建在什么位置?[生]码头应建在线段AB的垂直平分线与在A,B一侧的河岸边的交点上.[师]同学们认同他的看法吗?[生]是的[师]相信通过本节课的学习你们能帮助老师来解决这个问题,那么就让我们带着这个问题进入本节课的学习──线段的垂直平分线。Ⅱ.讲述新课线段垂直平分线的性质定理[师]回顾旧知1.什么叫做线段的垂直平分线?2.想一想,怎样画线段AB的垂直平分线。[师]动手操作:作线段AB的垂直平分线MN,垂足为C;在MN上任取一点P,连结PA、PB;量一量:PA、PB的长,你能发现什么?我们从刚才的观察猜想的过程中得到了线段垂直平分线的性质定理,大家知道这是不够的,还必须利用公理及已学过的定理推理、证明它.那么如何证明呢?[师](引导)问题一:①要证“线段垂直平分线上的点到线段两个端点的距离相等”,可线段垂直平分线上的点有无数多个,需一个一个依次证明吗?(强调)我们只需在线段垂直平分线上任取一点代表即可,因为线段垂直平分线上的点都具有相同的性质.(开始让学生有这样的数学思想)②你能根据定理画图并写出已知和求证吗?1③谁能帮老师分析一下证明思路?[生](思考回答)[师生共析]已知:如图,直线MN⊥AB,垂足是C,且AC=BC,P是MN上的点.求证:PA=PB.分析:要想证明PA=PB,可以考虑包含这两条线段的两个三角形是否全等.证明:∵MN⊥AB,∴∠PCA=∠PCB=90°.∵AC=BC,PC=PC,∴△PCA≌△PCB(SAS).∴PA=PB(全等三角形的对应边相等).[第二部分]线段垂直平分线的性质的应用随堂练习:【例1】:如图,在△ABC中,BC=12,AB的垂直平分线交BC边于点F,AC的垂直平分线交BC边于点H.求△AFH的周长。变式:在△ABC中,AB的垂直平分线交BC边于点F,AC的垂直平分线交BC边于点H.若∠B=35°,∠C=25°,则∠FAH=________.2.已知:如图,AB=AC,ÐA=30o,AB的垂直平分线MN交AC于D,则Ð1=,Ð2=.3.如图所示,在△ABC中,AB=AC=32,MN是AB的垂直平分线,且有BC=21,求△BCN的周长。4如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,AB,AC,CE的长度有什么关系?AB+BD与DE有什么关系?拓展演练:5.已知:如图,在△ABC中,AB>AC,∠BAC的平分线与BC的垂直平分线DM相交于点D,过点D作DE⊥AB于点E,DF⊥AC交AC的延长线于点F.ABCDE2求证:EB=FC.在△ABC中,AB的垂直平分线交BC边于点F,AC的垂直平分线交BC边于点H.若∠B=35°,∠C=25°,则∠FAH=________.Ⅳ.课时小结本节课我们先推理证明了线段的垂直平分线的性质定理和判定定理,并学会用尺规作线段的垂直平分线.Ⅴ.课后作业习题65页第6、10题Ⅵ.板书设计§1.3.1线段的垂直平分线(一)一、线段垂直平分线的定义.二、线段垂直平分线的性质定理.教学反思:本课我们安排的教学流程是:画直线的垂直平分线,研究和证明线段的垂直平分线的性质;体会线段垂直平分线的性质的应用。在对学生进行提升训练中,教师极力鼓励学生讲解并阐述理由,然后再引导学生结合图形体会到线段的垂直平分线的存在及性质,这样,既尊重了学生的学习兴趣,又符合学生的认知结构,并且结合图形掌握知识达成度较高。不足的地方:1.教师多放手让学生去讲解题,在讲完之后重点、适时的补充及点评。2.教师的几何语言应该更精准些。AFDBECM3