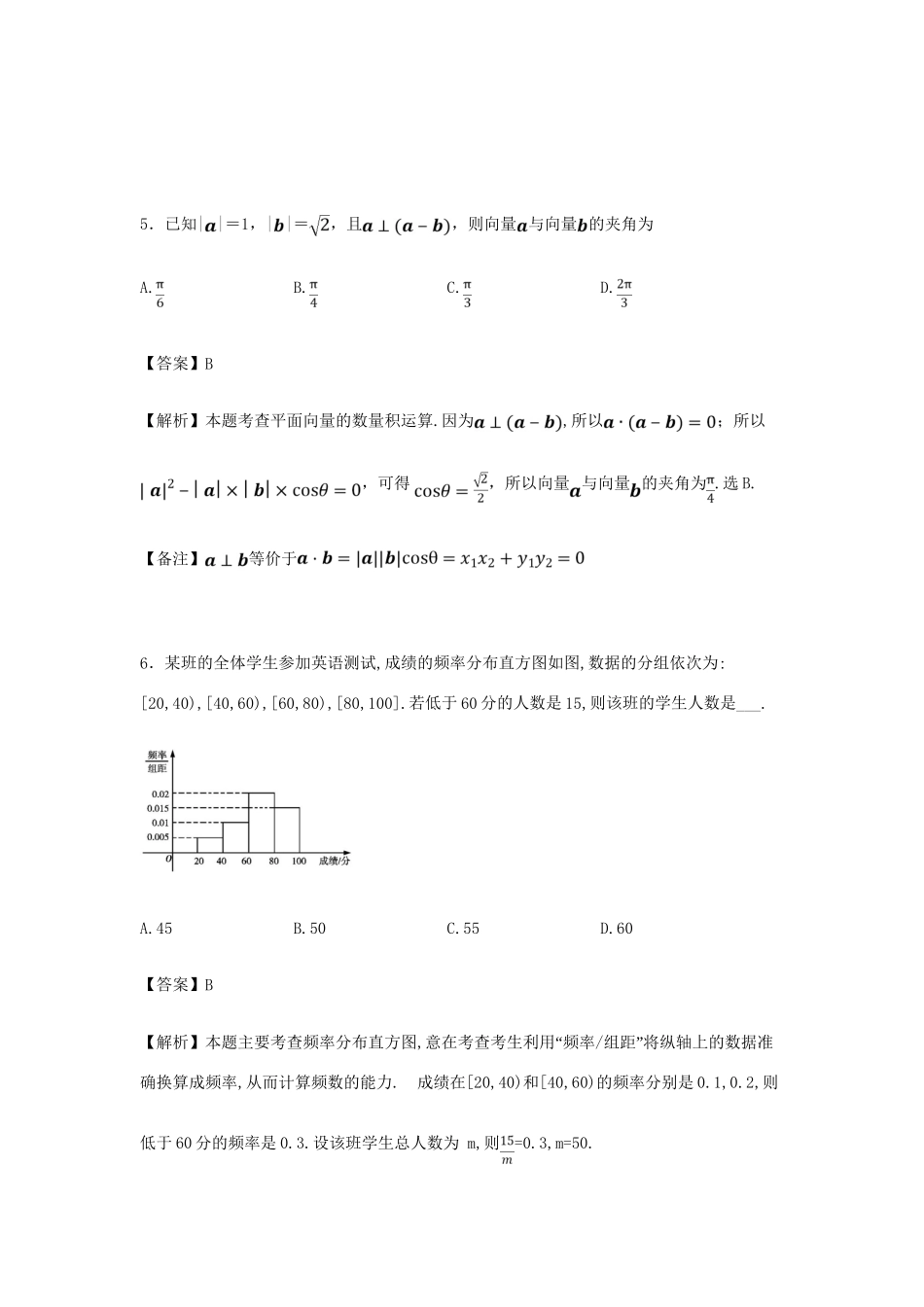
山西省康杰中学、临汾一中、忻州一中、长治二中届高三上学期第二次联考数学(理)一、选择题:共11题1.已知集合,集合,则等于A.B.C.D.【答案】A【解析】本题考查集合的基本运算.=,,所以.选A.2.i是虚数单位,若,则的值是A.2−B.1−C.0D.【答案】C【解析】本题考查复数的概念与运算,对数运算.==,所以,,所以=.选C.3.阅读如图的程序框图,运行相应的程序,若输入的值为1,则输出S的值为A.64B.73C.512D.585【答案】B【解析】本题考查流程图.第一次,,;第二次,;第三次,;所以输出.选B.4.已知等比数列中,各项都是正数,且成等差数列,则=A.B.C.D.【答案】C【解析】本题考查等差数列和等比数列的性质.因为成等差数列,所以a1+2a2;即a3=a1+2a2,整理得q2=1+2q,解得q=;而数列的各项都是正数,所以q=;所以=q2=.选C.5.已知||=1,||=,且,则向量与向量的夹角为A.B.C.D.【答案】B【解析】本题考查平面向量的数量积运算.因为,所以;所以,可得,所以向量与向量的夹角为.选B.【备注】等价于6.某班的全体学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100].若低于60分的人数是15,则该班的学生人数是___.A.45B.50C.55D.60【答案】B【解析】本题主要考查频率分布直方图,“意在考查考生利用频率/”组距将纵轴上的数据准确换算成频率,从而计算频数的能力.成绩在[20,40)和[40,60)的频率分别是0.1,0.2,则低于60分的频率是0.3.设该班学生总人数为m,则=0.3,m=50.7.“是函数在区间”内单调递增的A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件【答案】C【解析】本题考查函数的单调性、充要条件.当时,,其在区间内单调递增;当时,,其在区间内单调递增;当时,在区间“内有增有减;即函数在区间内单”调递增等价于;所以“是函数在区间内单调”递增的充分必要条件.选C.8.将函数的图像向左平移个单位长度后,所得到的图像关于y轴对称,则的最小值是A.B.C.D.【答案】A【解析】本题考查三角变换,三角函数的图像.函数图像向左平移()个单位后,可得,因为为偶函数,所以;因为,所以的最小值是.选A.【备注】辅助角公式:9.已知=,则等于A.-5B.5C.90D.180【答案】D【解析】本题考查二项式定理的应用.因为=;因为,所以.选D.【备注】二项展开式的通项公式:.10.设抛物线的焦点为,点在上,,若以为直径的圆过点,则的方程为A.或B.或C.或D.或【答案】C【解析】 抛物线C方程为y2=3px(p>0),∴焦点F坐标为(,0),可得|OF|=, 以MF为直径的圆过点(0,2),∴设A(0,2),可得AF⊥AM,Rt△AOF中,|AF|=,∴sin∠OAF=, 根据抛物线的定义,得直线AO切以MF为直径的圆于A点,∴∠OAF=∠AMF,可得Rt△AMF中,sin∠AMF=, |MF|=5,|AF|=,∴,整理得4+=,解之可得p=或p=,因此,抛物线C的方程为或,故选C.11.已知函数与的图象上存在关于轴对称的点,则的取值范围是A.B.C.D.【答案】B【解析】本题考查指数、对数函数,函数与方程.由题意得:存在,使得成立,即在区间上有解;构造函数,而单增,且当时,;当,时,;由零点存在定理可得:在区间上有零点,即在区间上有解;当时,,解得;所以的取值范围是.选B.二、填空题:共4题12.定积分=.【答案】【解析】本题考查定积分的几何意义.表示以原点为圆心,以4为半径的圆的面积的,所以=.13.已知满足约束条件,求的最小值是.【答案】【解析】本题考查线性规划问题.画出可行域(如图三角形所示),:;表示到区域内点的距离的平方;当圆D与直线相切时,取得最小值;,所以的最小值为.【备注】体会数形结合思想.14.若三棱锥P-ABC的最长的棱,且各面均为直角三角形,则此三棱锥的外接球的体积是.【答案】【解析】本题考查空间几何体的结构特征与体积.三棱锥P-ABC如图所示,其四个顶点全部位于正方体的顶点处,其中为正方体的对角线;而正方体的外接球半径,即三棱锥的外接球半径;所以此三棱锥的外接球的体积.【备注】体会数形结合思想.15.已知数列{an}满足a1=1,an+1·an=2n(n∈N*),则S=______.【答案】【解析】本题考查数列求和.由题意得,,,,而,所以;当为奇数时,数列{an}是以为首项、为公比的等比数列,...