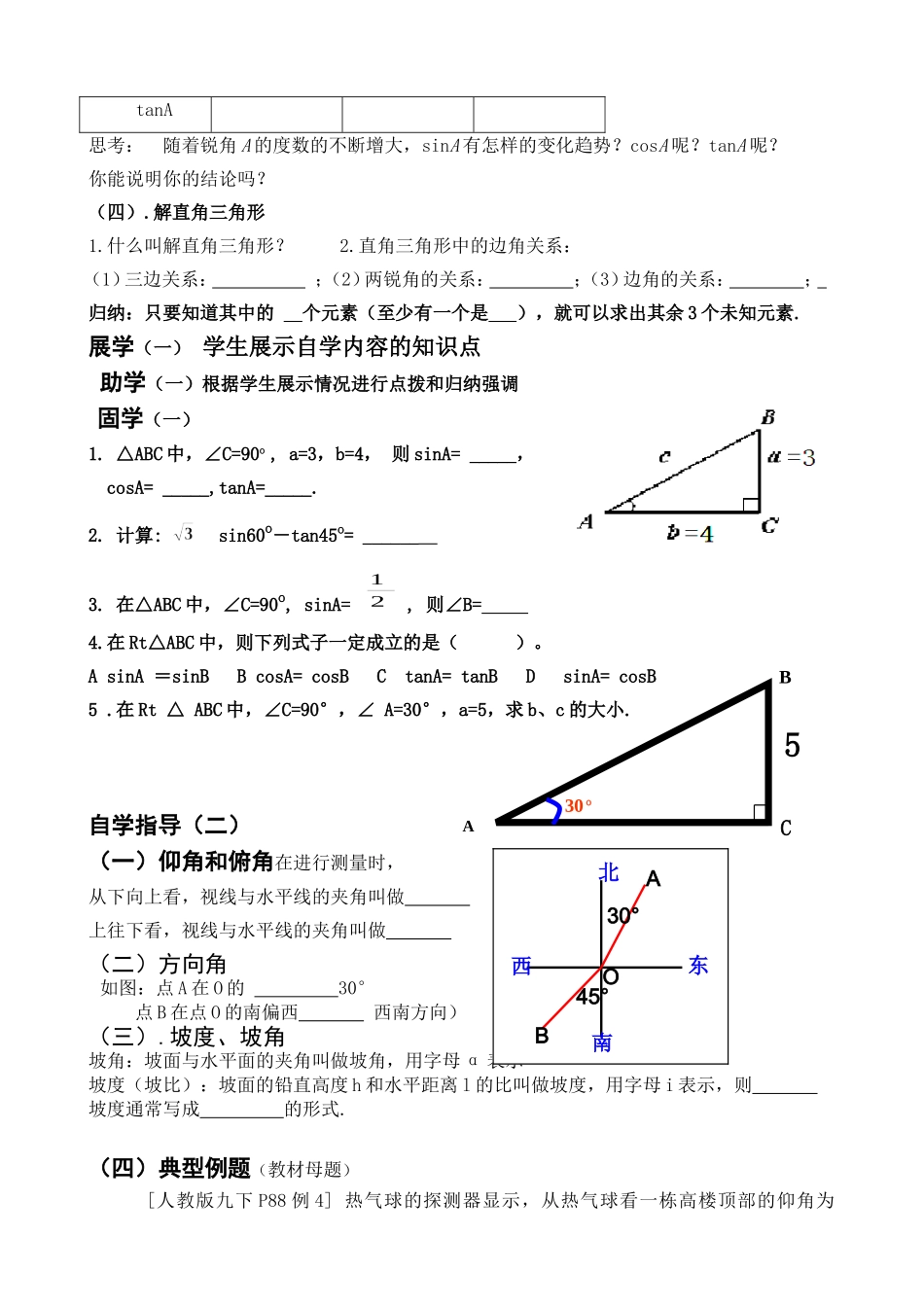
锐角三角函数复习课执教者:韦素珍班级:091班【考向聚焦】:结合近年中考试题分析,锐角三角函数的内容考查主要有以下特点:1.命题方式为锐角三角函数的定义、性质的应用、特殊角三角函数值的求法,运用锐角三角函数解决与直角三角形有关的实际问题.题型有选择题、填空题、解答题,多以中低档题出现2.命题的热点为根据题中给出的信息构建图形,建立数学模型,然后用解直角三角形的知识解决问题.复习目标:1.通过复习进一步巩固锐角三角函数的定义,并能灵活运用定义进行有关计算。2.通过复习牢记特殊角的三角函数值,并能进行有关计算。3.通过复习进一步巩固直角三角形的边角关系,并能进行解直角三角形的知识应用。重点:特殊角的三角函数值,并能进行有关计算;解直角三角形的知识应用。难点:解直角三角形的知识应用。教学过程自学指导(一)(一).锐角三角函数的概念正弦:把锐角A的对边与斜边的比叫做∠A的正弦,记作余弦:把锐角A的邻边与斜边的比叫做∠A的余弦,记作正切:把锐角A的对边与邻边的比叫做∠A的正切,记作锐角A的正弦、余弦、正切都叫做(二)、锐角三角函数的性质1.若∠A为锐角,则有sinA=cos(90°一A)=cosA=sin(90°一A)=2.同角三角函数的关系:(1)平方关系:sin2A+cos2A=(2)商数关系:sinA/cosA=(三)、特殊角的三角函数值三角函数30°45°60°siaAcosAcbCaABccctanA思考:随着锐角A的度数的不断增大,sinA有怎样的变化趋势?cosA呢?tanA呢?你能说明你的结论吗?(四).解直角三角形1.什么叫解直角三角形?2.直角三角形中的边角关系:(1)三边关系:;(2)两锐角的关系:;(3)边角的关系:;归纳:只要知道其中的个元素(至少有一个是),就可以求出其余3个未知元素.展学(一)学生展示自学内容的知识点助学(一)根据学生展示情况进行点拨和归纳强调固学(一)1.△ABC中,∠C=90o,a=3,b=4,则sinA=_____,cosA=_____,tanA=_____.2.计算:sin60o-tan45o=______3.在△ABC中,∠C=90o,sinA=21,则∠B=4.在Rt△ABC中,则下列式子一定成立的是()。AsinA=sinBBcosA=cosBCtanA=tanBDsinA=cosB5.在Rt△ABC中,∠C=90°,∠A=30°,a=5,求b、c的大小.自学指导(二)(一)仰角和俯角在进行测量时,从下向上看,视线与水平线的夹角叫做上往下看,视线与水平线的夹角叫做(二)方向角如图:点A在O的30°点B在点O的南偏西西南方向)(三).坡度、坡角坡角:坡面与水平面的夹角叫做坡角,用字母α表示坡度(坡比):坡面的铅直高度h和水平距离l的比叫做坡度,用字母i表示,则坡度通常写成的形式.(四)典型例题(教材母题)[人教版九下P88例4]热气球的探测器显示,从热气球看一栋高楼顶部的仰角为ABC30o530°45°BOA东西北南30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高?(结果保留小数点后一位)图25-6展学(二)学生回答自学内容的知识点助学(二)根据学生展示情况进行点拨和建立数学模型固学(二)(2011·柳州市中考)操场里有一个旗杆,老师让小明去测量旗杆高度,小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为30度,并已知目高为1.65米.然后他很快就算出旗杆的高度了(保留0.01,)。你想知道小明怎样算出的吗?侧学(直击中考)1.(2011·乐山中考)如图,在4×4的正方形网格中,tanα=()10米1.65米30°?31.73=(A)1(B)2(C)12(D)2.(2011·北海市中考)如图(1),已知:45°
cosA(C)sinA>tanA(D)sinA