离散时间系统VIP免费

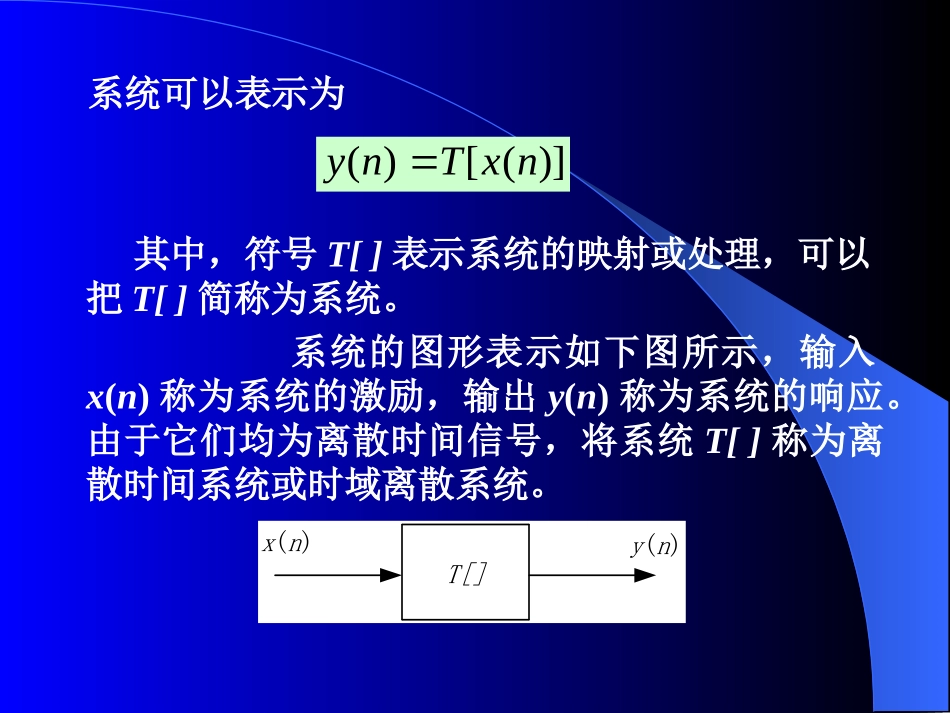
五、离散时间系统；六、LSI系统输入、输出关系；七、LSI系统的频率响应；八、确定性信号的相关函数SectionB离散时间系统基础1.51.5离散时间系统离散时间系统1.系统定义数字信号处理的任何处理都是依靠系统来完成的,所以系统是数字信号处理的核心，系统一般包括系统硬件和系统所完成的处理算法。系统在数学上定义为将输入序列x(n)映射成输出序列y(n)的唯一性变换或运算。这种映射是广义的，实际上表示的是一种具体的处理，或是变换，或是滤波。系统可以表示为其中，符号T[]表示系统的映射或处理，可以把T[]简称为系统。系统的图形表示如下图所示，输入x(n)称为系统的激励，输出y(n)称为系统的响应。由于它们均为离散时间信号，将系统T[]称为离散时间系统或时域离散系统。)]([)(nxTnyT[]x(n)y(n)2.线形离散时间系统满足叠加原理的系统，或满足齐次性和可加性的系统称为线性系统。设y1(n)=T[x1(n)]，y2(n)=T[x2(n)]对任意常数a,b，若T[ax1(n)+bx2(n)]=aT[x1(n)]+bT[x2(n)]=ay1(n)+by2(n)则称T[]为线性离散时间系统。推广到一般情况，设yk(n)=T[xk(n)]，k=1，2，...N线性系统满足1≤k≤N线性系统的特点是多个输入的线性组合的系统输出等于各输入单独作用的输出的线性组合。NkNkNkkkkkkknyanxTanxaT111)()]([)]([[例1]证明由线性方程表示的系统是非线性系统。证明设所以，该系统是非线性系统。()(),ynaxnbab为常数111222()[()]()()[()]()ynTxnaxnbynTxnaxnb1212[()()][()()]Txnxnaxnxnb1212()()()()axnaxnbynyn不满足可加性3.非时变离散时间系统若满足下列条件，系统称为非时变（非移变）系统，或时不变（移不变）系统。设y(n)=T[x(n)]对任意整数k,有y(n-k)=T[x(n-k)]即系统的映射T[]不随时间变化，只要输入x(n)是相同的，无论何时进行激励，输出y（n）总是相同的，这正是系统非时变性的特征。下图形象说明了系统非时变性的概念。T[]nn4x(n)0123-1-2x(n-2)0123456nn44y(n)y(n-2)0011223356756789[例2]设系统的映射y=T[x(n)]=nx(n)，判断系统的线性和时不变性。解设y1(n)=nx1(n),y2(n)=nx2(n)a1x1(n)+a2x2(n)=x(n)则T[x(n)]=nx(n)=na1x1(n)+na2x2=a1y1(n)+a2y2(n)所以，系统为线性系统。设y(n)=nx(n),x1(n)=x(n-k)y1(n)=nx1(n)=nx(n-k)而y(n-k)=(n-k)x(n-k)≠y1(n)所以，系统为时变系统。4.线性时不变离散系统定义同时具备线性和时不变性的系统称作线性非时变系统或线性时不变系统。它的重要意义在于，系统的处理过程可以统一采用这种系统的特征描述之一——单位采样响应，以一种相同的运算方式——卷积运算，进行统一的表示。任何一个信号可以表示成单位采样序列的线性组合，即kknkxnx)()()(系统对的响应为设系统对单位采样序列的响应为，即称为系统的“单位采样响应”，它是描述系统的一个非常重要的信号。)(nxkknkxTnxTny)]()([)]([)(kknTkx)]([)()(n)(nh)]([)(nTnh根据时不变性，有则系统输出y(n)可表示为上式表明：当线性时不变系统的单位采样响应h(n)确定时，系统对任何一个输入x(n)的响应y(n)就确定了，y(n)可以表示成x(n)和h(n)之间的一种简单的运算形式。将上式的运算方式称作“离散卷积”，简称“卷积”，采用符号“*”表示，即)]([)(knTknhkknhkxny)()()()(*)()(nhnxny)(*)(nxnh5.离散卷积的计算卷积的计算一般采用两种方法：解析法和图解法，或是两种方法的结合。[例2.3]设线性时不变系统的单位脉冲响应和输入序列如下图所示，画出输出的波形。01234n210.5h(n)012341-12nx(n)解（1）采用图解法。0()()()()()mynxnhnxmhnm图解法的过程如图2.2所示。(a)x(m)-10-1-211232mx(m)(b)n=00.5m0123-1-221h(0-m)0123-1-2210.5mh(1-m)(c)n=1m0123-1-2120.5h(2-m)(d)n=20123-1-2210.5mh(-1-m)(e)n=-1m012-13-2-3-4210.5h(-2-m)(f)n=-2-2-20123456-1-1-0.521214.5ny(n)(g)y(n)图2.2例2.2图解法(a)x(m)-10-1-211232mx(m)(b)n=00.5m0123-1-221h(0-m)0123-1-2210.5mh(1-m)(c)n=1（2）采用解析法。因为所以将x(n)的表达式代入上式，得...