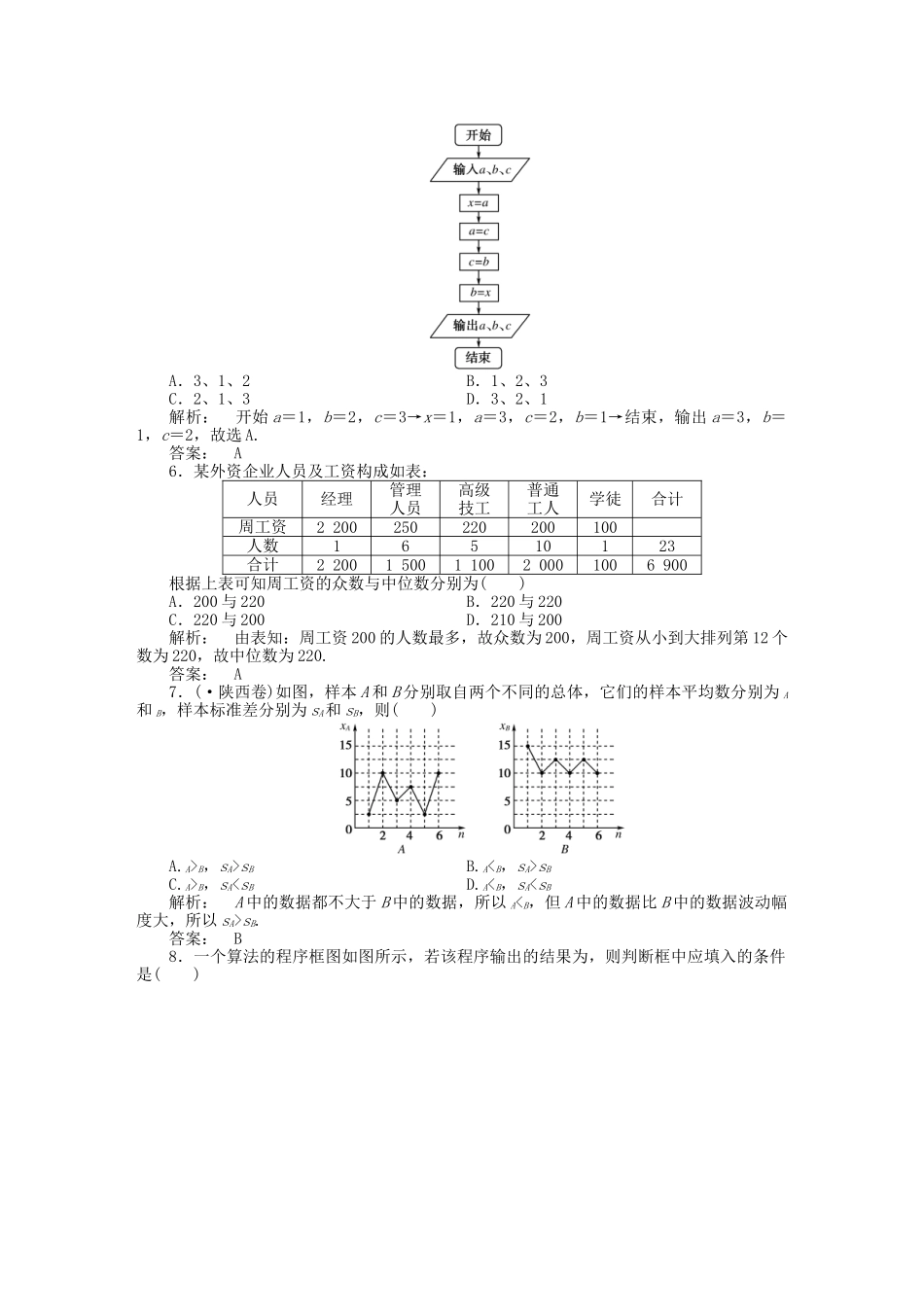
章末优化训练(算法初步与框图统计、统计案例概率)(本栏目内容,在学生用书中以活页形式分册装订!)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.对变量x,y有观测数据(xi,yi)(i=1,2…,,10),得散点图1;对变量u、v有观测数据(ui,vi)(i=1,2…,,10),得散点图2.由这两个散点图可以判断()A.变量x与y正相关,u与v正相关B.变量x与y正相关,u与v负相关C.变量x与y负相关,u与v正相关D.变量x与y负相关,u与v负相关解析:夹在带状区域内的点,总体呈上升趋势的属于正相关;反之,总体呈下降趋势的属于负相关.显然选C.答案:C2.某商场有四类食品,其中粮食类、植物油类、动物性食品类及果蔬类分别有40种、10种、30种、20种,现从中抽取一个容量为20的样本进行食品安全检测.若采用分层抽样的方法抽取样本,则抽取的植物油类与果蔬类食品种数之和是()A.4B.5C.6D.7解析:共有食品100种,抽取容量为20,所以各抽取,故抽取植物油类与果蔬类食品种数之和为10×+20×=6,所以选C.答案:C3.在一底面半径和高都是2m的圆柱形容器中盛满小麦种子,但有一粒带麦锈病的种子混入了其中.现从中随机取出2m3的种子,则取出带麦锈病的种子的概率是()A.B.C.D.1-解析:可用体积作为几何度量,易知取出带有麦锈病的种子的概率为P==.答案:C4.如图表示甲、乙两名篮球运动员每场比赛得分情况的茎叶图,则甲和乙得分的中位数的和是()A.56分B.57分C.58分D.59分解析:由图可知甲的中位数为32,乙的中位数为25,故和为57.故选B.答案:B5.阅读下边的程序框图,若输入的a、b、c分别是1、2、3,则输出的a、b、c分别是()A.3、1、2B.1、2、3C.2、1、3D.3、2、1解析:开始a=1,b=2,c=3→x=1,a=3,c=2,b=1→结束,输出a=3,b=1,c=2,故选A.答案:A6.某外资企业人员及工资构成如表:人员经理管理人员高级技工普通工人学徒合计周工资2200250220200100人数16510123合计22001500110020001006900根据上表可知周工资的众数与中位数分别为()A.200与220B.220与220C.220与200D.210与200解析:由表知:周工资200的人数最多,故众数为200,周工资从小到大排列第12个数为220,故中位数为220.答案:A7.(·陕西卷)如图,样本A和B分别取自两个不同的总体,它们的样本平均数分别为A和B,样本标准差分别为sA和sB,则()A.A>B,sA>sBB.AsBC.A>B,sAsB.答案:B8.一个算法的程序框图如图所示,若该程序输出的结果为,则判断框中应填入的条件是()A.i≥5?B.i≥6?C.i<5?D.i<6?解析:由框图知S=0+1…-+++=1-=.∴i=5,∴应填入i<6?.答案:D9.已知集合M={(x,y)|x+y≤8,x≥0,y≥0},N={(x,y)|x-3y≥0,x≤6,y≥0},若向区域M内随机投一点,则点P落入区域N的概率为()A.B.C.D.解析:在平面直角坐标系中分别画出区域M和N,可计算得区域M和N的面积分别等于S=×8×8=32,S′=×6×2=6,所以点P落入区域N的概率P==.答案:D10.(·东北三校三模)如图,若依次输入的x分别为π、,相应输出的y分别为y1、y2,则y1、y2的大小关系是()A.y1=y2B.y1>y2C.y1cos成立,所以输出的y1=sin=;当输入的x为时,sin>cos不成立,所以输出的y2=cos=,所以y10,所以f(x)在R上递增,若f(x)在[1,2]上有零点,则需经验证有(1,2)、(1,4)、(1,8)、(2,4)、(2,8)、(2,12)、(3,4)、(3,8)、(3,12)、(4,8)、(4,12)共11对满足条件,而总的情况有CC=16种,故所求概率为,...