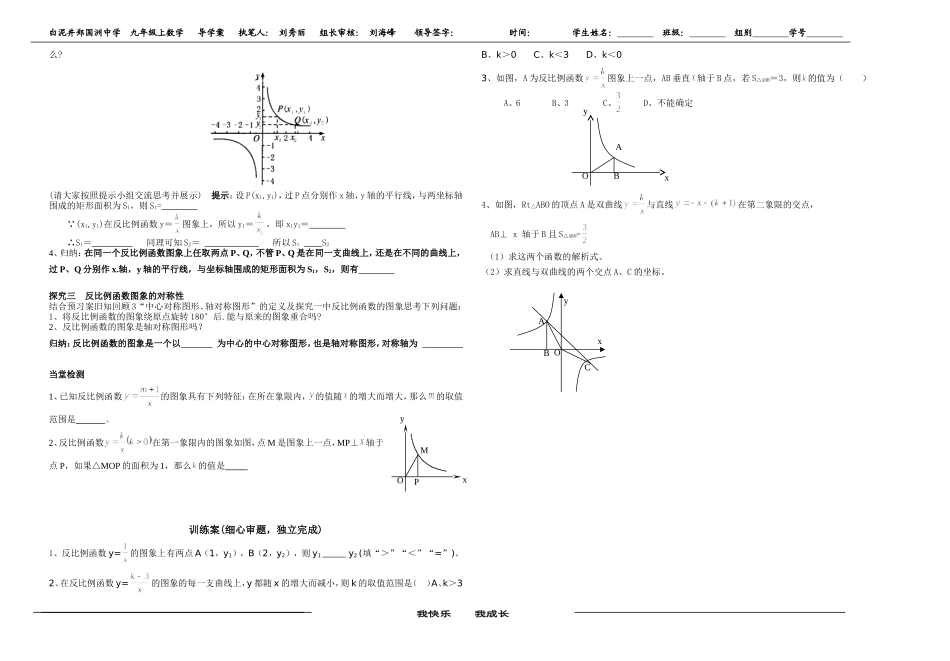
白泥井郑国洲中学九年级上数学导学案执笔人:刘秀丽组长审核:刘海峰领导签字:时间:学生姓名:班级:组别学号课题第五章《反比例函数》5.2反比例函数的图象与性质(第2课时)学习目标1、知识与技能(1)基本目标进一步巩固反比例函数图象的画法。(2)中层目标掌握反比例函数的主要性质。(3)发展目标反比例函数性质的应用。2、过程与方法通过观察反比例函数的图象,归纳其性质,训练学生的识图能力,语言组织能力,让学生体会数形结合的思想。3、情感态度与价值观关注学生对问题分析过程的思考,培养和发扬学生合作交流的团队精神。学习重点反比例函数的主要性质。学习难点反比例函数性质的应用。预习案(新旧链接,温故知新)一、旧知回顾1、反比例函数图象的形状是。2、反比例函数图象所在的象限由决定,当时,两支双曲线分别位于第象限内;当时,两支双曲线分别位于第象限内。3、中心对称图形、轴对称图形的定义是如何叙述的?二、预习自测1、反比例函数y=-的图象在第象限,在每个象限内,y随x的增大而。2、如图,正方形的边长为2,反比例函数过点,则的值是()A.B.C.D.三、本课时预习后我的疑惑探究案(大胆质疑,勇敢展示)探究一、反比例函数的增减性1、观察反比例函数y=,y=,y=的图象,它们有什么共同点?思考提示:(1)函数图象分别位于哪几个象限?(5、6号同学回答)(2)当x取什么值时图象在第一象限?当x取什么值时图象在第三象限?(3、4号)(3)在每一个象限内,随着x值的增大,y的值是怎样变化的?为什么?(1、2号)2、下面用类推的方法来研究y=-,y=-,y=-的图象有哪些共同特征?3、通过以上问题,我们可以归纳如下结论:反比例函数y=的图象,当k>0时,在每一象限内,y的值随x值的增大而;当k<0时,在每一象限内,y的值随x值的增大而探究二、反比例函数y=(k≠0)中k的几何意义在一个反比例函数图象上任取两点P、Q,过点P分别作x轴、y轴的平行线,与坐标轴围成的矩形面积为S1;过点Q分别作x轴、y轴的平行线,与坐标轴围成的矩形面积为S2。S1与S2有什么关系?为什我快乐我成长xyCOAByxOPM白泥井郑国洲中学九年级上数学导学案执笔人:刘秀丽组长审核:刘海峰领导签字:时间:学生姓名:班级:组别学号么?(请大家按照提示小组交流思考并展示)提示:设P(x1,y1),过P点分别作x轴,y轴的平行线,与两坐标轴围成的矩形面积为S1,则S1=∵(x1,y1)在反比例函数y=图象上,所以y1=,即x1y1=∴S1=同理可知S2=所以S1S24、归纳:在同一个反比例函数图象上任取两点P、Q,不管P、Q是在同一支曲线上,还是在不同的曲线上,过P、Q分别作x.轴,y轴的平行线,与坐标轴围成的矩形面积为S1,S2,则有探究三反比例函数图象的对称性结合预习案旧知回顾3“中心对称图形、轴对称图形”的定义及探究一中反比例函数的图象思考下列问题:1、将反比例函数的图象绕原点旋转180°后.能与原来的图象重合吗?2、反比例函数的图象是轴对称图形吗?归纳:反比例函数的图象是一个以为中心的中心对称图形,也是轴对称图形,对称轴为当堂检测1、已知反比例函数的图象具有下列特征:在所在象限内,的值随的增大而增大,那么的取值范围是。2、反比例函数在第一象限内的图象如图,点M是图象上一点,MP⊥轴于点P,如果△MOP的面积为1,那么的值是训练案(细心审题,独立完成)1、反比例函数y=的图象上有两点A(1,y1),B(2,y2),则y1y2(填“>”“<”“=”)。2、在反比例函数y=的图象的每一支曲线上,y都随x的增大而减小,则k的取值范围是()A、k>3B、k>0C、k<3D、k<03、如图,A为反比例函数图象上一点,AB垂直轴于B点,若S△AOB=3,则的值为()A、6B、3C、D、不能确定4、如图,Rt△ABO的顶点A是双曲线与直线在第二象限的交点,AB⊥x轴于B且S△ABO=(1)求这两个函数的解析式。(2)求直线与双曲线的两个交点A、C的坐标。我快乐我成长OyxBACABOxy