指数函数的图象及其性质VIP免费

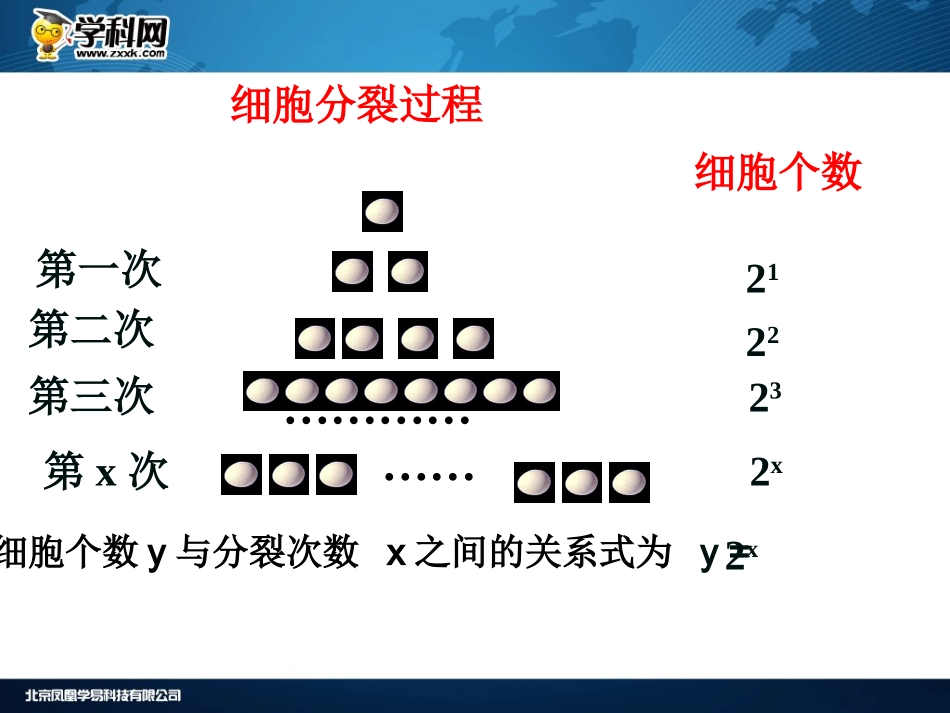
指数函数的图象及其性质（一）zxxk材料1:某种细胞分裂时,由1个分裂成2个,2个分裂成4个…一个这样的细胞分裂x次后,得到的细胞分裂的个数y与x的函数关系是什么?一、创设情境，形成概念细胞分裂过程zx`xk细胞个数第一次第二次第三次212322…………第x次……2x细胞个数y与分裂次数x之间的关系式为y=2x材料2：将一纸条第一次截去它的一半,第二次截去剩余部分的一半，第三次截去第二次剩余部分的一半，依次截下去,问截的次数与剩下的纸条之间的关系.次数长度1次2次3次4次……43322)21(21)21()21(21)21()21(212121该纸条截x次后，得到的长度y与x的关系式是xy)21(x次xx)21(21)21(1xayxR形如的函数叫做指数函数，z``xxk为自变量，定义域为其中指数为自变量幂为函数底为常数,a(0)a1且为后面研究函数图象性质埋下伏笔为后面研究函数图象性质埋下伏笔xy2xy)21(指数函数的概念：指数函数概念一般地，函数叫做指数函数，其中x是自变量，函数的定义域是R，值域是(0,+∞).为什么要规定a>0,且a≠1呢？①若a=0，则当x>0时，xa=0；0时，xa无意义.当x②若a<0，则对于x的某些数值，可使xa无意义.如③若a=1，则对于任何xR，xa=1，是一个常量，没有研究的必要性.为了便于研究，规定：a>0,且a≠1在规定以后，对于任何xR，xa都有意义，且xa>0.因此指数函数的定义域是R，值域是(0,+∞).1(2)2xyx在时就没有意义。xayxR定义：函数叫做指数函数，为自变量，定义域为其中)aa(10且下列函数中，哪些是指数函数？xy44xyxy414xy我是我是我不是我还不是你答对了吗？我不是应用举例：二、发现问题，探求新知二、发现问题，探求新知•怎样得到指数函数图像?•指数函数图像的特点?Z``xxk•通过图像，你能发现指数函数的哪些性质?作函数图象xy2xy)21(作函数图象x-10123y1248x-3-2-101y84212121xy2xy)21(xy2xy3xyo123-1-2-3XOYxy)31(xy)21(xy)21(XOYY=1y=3Xy=2xxy)31(通过作图，我们发现y=ax的图象大致分两种类型，即0＜a＜1和a＞1，图象如下：zx``xkxy(0,1)y=1y=ax(a＞1)0xyy=1y=ax(0＜a＜1)(0,1)0y=ax图象性质xyo1xyo1R(0,+∞)过定点(0,1)，即x=0时，y=1当x＞0时，y＞1当x＜0时，0＜y＜1当x＞0时，0＜y＜1当x＜0时，y＞1在R上是增函数在R上是减函数(1)定义域(2)值域(3)定点(5)函数值的分布情况(4)单调性指数函数的图象和性质a＞10＜a＜101xyxy2xy21xy3xy31xy31xy21三、深入探究，加深理解三、深入探究，加深理解引导学生观察图像，发现图像与底的关系引导学生观察图像，发现图像与底的关系在第一象限沿箭头方向底增大在第一象限沿箭头方向底增大底互为倒数的两个函数图像关于y轴对称底互为倒数的两个函数图像关于y轴对称()xxfa例1.已知指数函数经过点（3，π），求f(0)、f(1)、f(-3)的值.(0),(1),(3)fff分析：要求的值，需要我们先求出指数函数的解析式。根据函数图像经过（3，）这一条件，可以求得底数a的值。1333,,().xaafx即解得于是(a>0,且a≠1）的图象x解：因为指数函数y=a的图像经过点（3，），所以(3).f101331(0)1(1)(3).fff所以，，，四、当堂训练，共同提高①、2.531.7,1.7②、③、0.33.11.7,0.9328.0;8.0例2.比较下列各式大小①、2.531.7,1.7②、③、0.33.11.7,0.9328.0;8.0例2.比较下列各式大小zx```xk解.（1）35.27.1.71,35.2R7.1上是增函数；在函数xy①、2.531.7,1.7②、③、0.33.11.7,0.9328.0;8.0328.00.832R8.0上是减函数；在函数xy例2.比较下列各式大小解.（1）35.27.1.71,35.2R7.1上是增函数；在函数xy)2(①、2.531.7,1.7②、③、0.33.11.7,0.90.33.11.70.9328.0;8.0328.00.832R8.0上是减函数；在函数xy19.09.017.1.7101.303.0而由指数函数性质知：例2.比较下列各式大小解.（1）35.27.1.71,35.2R7.1上是增函数；在函数xy)2()3(同底指数幂比较大小，构造指数函数，利用函数单调性同底指数幂比较大小...