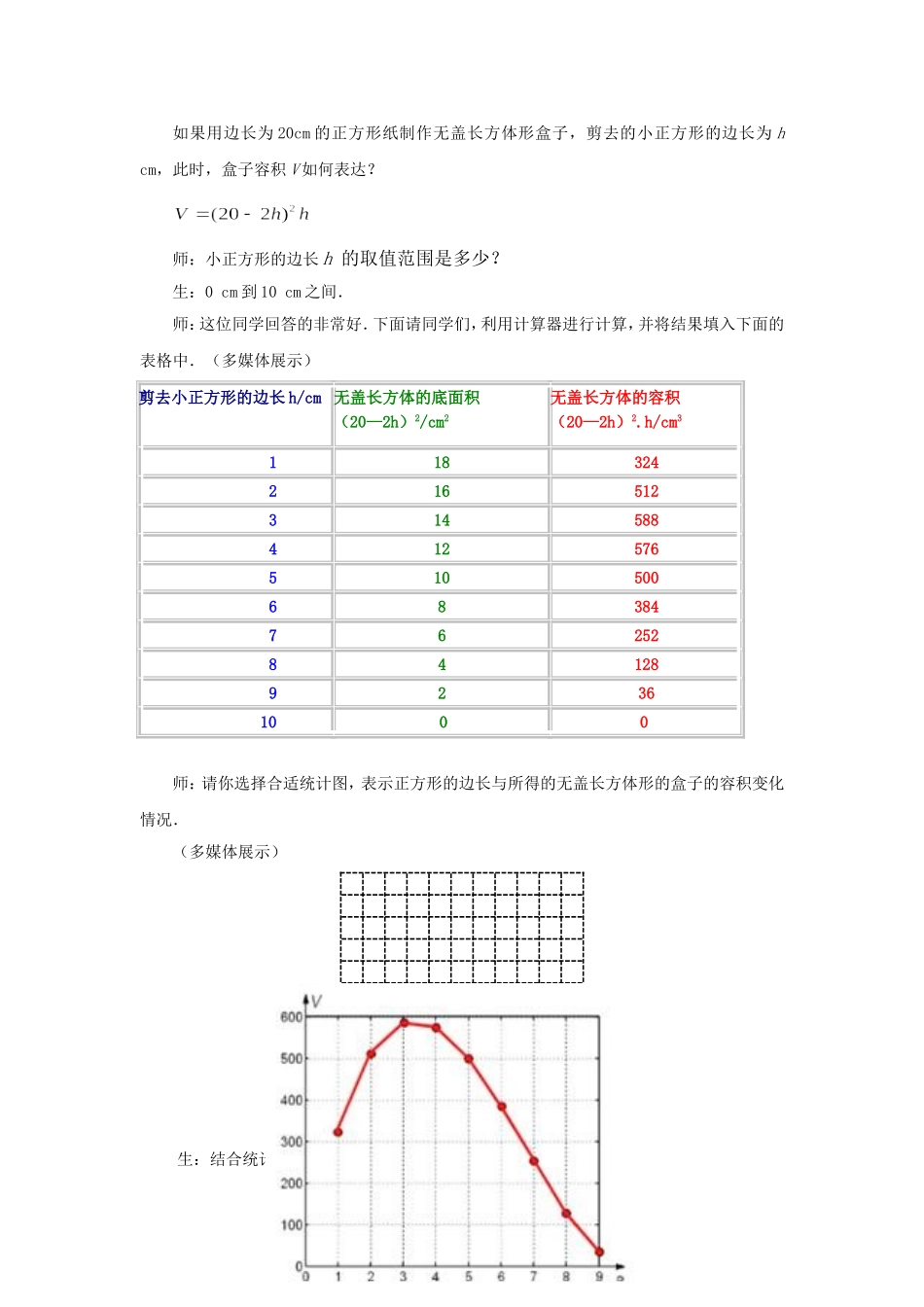
课题:综合与实践制作一个尽可能大的无盖长方体形盒子(新授课)教学目标:1.引导学生通过观察、猜想、操作、抽象、交流、合作、推理与反思等一系列活动,感受从实际问题抽象出数学问题---建立数学模型----综合应用已有的知识解决问题的过程.2.在解决问题的过程中进一步丰富学生的空间观念和符号感,通过借助自己拥有的信息去推断事物的变化趋势的活动,发展学生的推理能力.3.让学生获得一些初步的做数学实验的方法和经验.体验数学活动充满着探索与创造,通过获得成功的体验和克服困难的经历,增进应用数学的自信心.教学重点与难点:重点:引导学生探索如何设计制作尽可能大的无盖长方体形盒子.难点:感受数量之间相依变化的状态和趋势,体验分割逼近的方法和从特殊到一般的探究过程.教法及学法指导:本节课让学生能够比较完整地经历从具体情境中抽象出数学问题,然后对数学问题进行研究解决,在利用数学知识解决问题的过程.在整个教学过程中,学生进行小组合作活动,在活动中体现自主、合作、探究的学习方式.课前准备:教师准备:20×20cm卡纸若干,剪刀、直尺、透明胶布、多媒体课件.学生准备:学生课前用20×20cm正方形卡纸尝试制作一个无盖的长方体形盒子.教学过程:一、创设情境,导入新课你能帮我吗?同学们,我们班级的粉笔盒坏了,现在老师这里只有一张正方形的铁皮.你能帮帮老师,利用它制作一个无盖的长方体形粉笔盒吗?这节课我们就来研究如何制作一个尽可能大的无盖长方体形盒子.(板书课题)二、动手实践,探索规律活动一、制作无盖长方体形盒子同学们课前已经用一张边长为20cm的正方形卡纸制作了一个无盖的长方体体盒子,那么,你是如何做的呢?(制作一个无盖的长方体形盒子的方法很多,可以让学生积极发言,师生共同评价.)同学们的方法各不相同,不过基本思路都一样,就是在正方形的四个角上各剪去一个同样大小的正方形,然后沿着虚线折起来,就得到了一个无盖的长方体形盒子.(多媒体展示)小组内每一个人拿出用事先做好的无盖长方体盒子,比一比,谁的长方体盒子体积大?(教师演示比较盒子体积大小的方法)随着剪去的小正方形的边长的变化,所折无盖长方体形盒子的体积也会变化?那么到底是如何变化的呢?当剪去小正方形的边长为多少时,无盖长方体的体积最大?这节课我们来探究这个问题活动二、盒子容积的代数式表达如果大正方形的边长为a,剪掉小正方形的边长为h,用a和h来表示这个无盖长方体的容积V吗?生:交流讨论,并完成下面的填空.(多媒体展示)(1)折成的无盖长方体形纸盒高是.(2)折成的无盖长方体形纸盒的底面积是.(3)折成的无盖长方体形纸盒的容积V=.我得到的关系式是.活动三、分组合作,探究体积变化aha-2hha-2hhV如果用边长为20cm的正方形纸制作无盖长方体形盒子,剪去的小正方形的边长为hcm,此时,盒子容积V如何表达?师:小正方形的边长h的取值范围是多少?生:0cm到10cm之间.师:这位同学回答的非常好.下面请同学们,利用计算器进行计算,并将结果填入下面的表格中.(多媒体展示)剪去小正方形的边长h/cm无盖长方体的底面积(20—2h)2/cm2无盖长方体的容积(20—2h)2.h/cm311832421651231458841257651050068384762528412892361000师:请你选择合适统计图,表示正方形的边长与所得的无盖长方体形的盒子的容积变化情况.(多媒体展示)生:结合统计表,小组合作制作统计图.(多媒体展示)师:观察统计表和统计图,当小正方形边长变化时,所得到的无盖长方体形的盒子的容积是如何变化的?生:可以看出,当小正方形边长从1cm逐渐增大到3cm时,无盖长方体形盒子的容积逐渐增大;其后随着小正方形边长的增加容积逐渐减小;当小正方形边长为10cm时,容积为0cm3.师:当小正方形边长取什么值时,所得到的无盖长方体形盒子的容积最大?最大是多少?生:当小正方形边长为3cm时,容积最大,为588cm3.师:你同意他的看法吗?为什么?生:不同意.我通过折线统计图发现,当小正方形的边长为3cm时,盒子的容积并不是最大的,而应该是当小正方形的边长在3—4cm之间时,盒子的容积最大.师:我们发现,当小正方形的边长在3—4cm之...