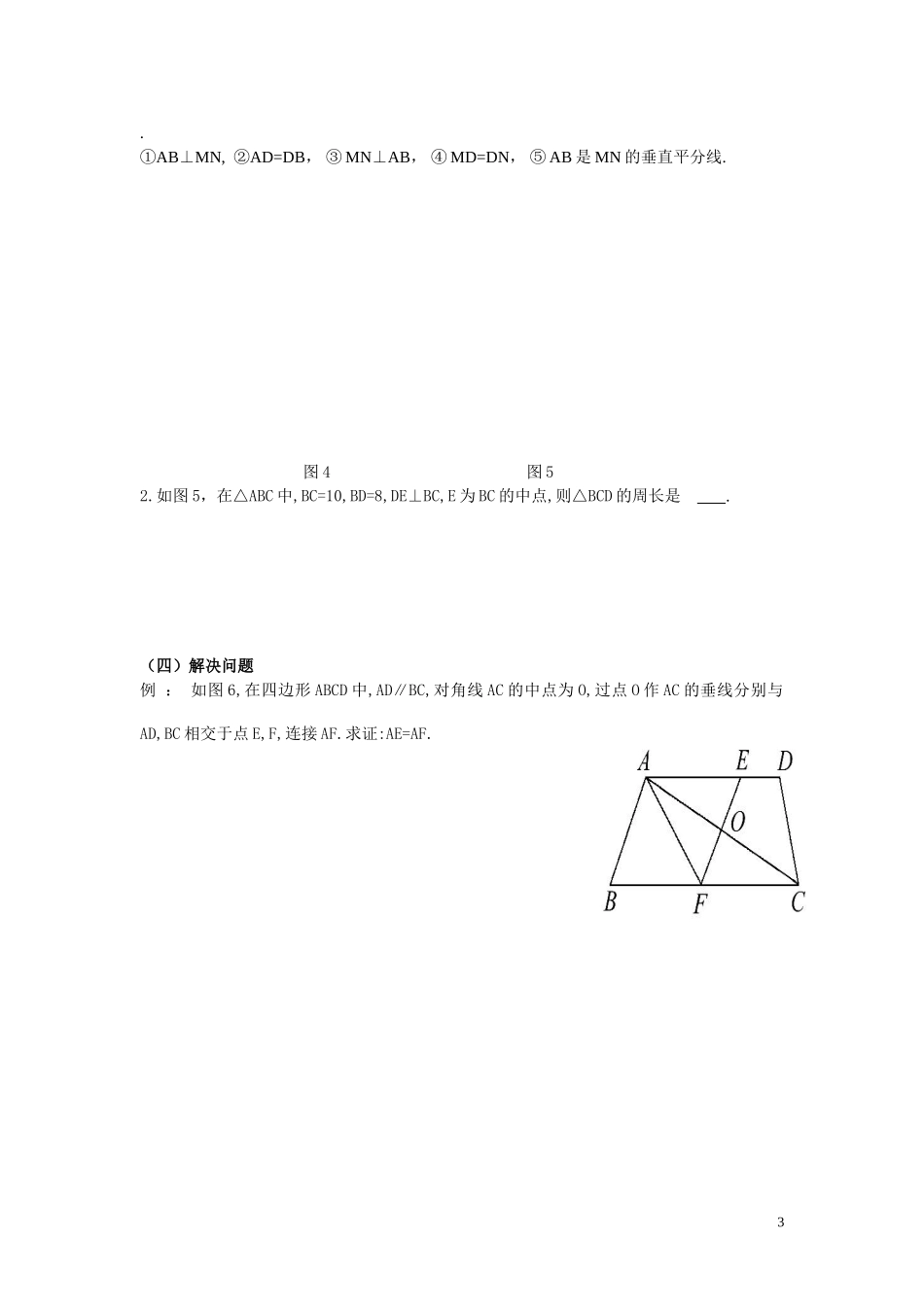
教学过程设计(一)复习与思考问题1:线段的垂直平分线的定义是什么?问题2:角平分线的性质是什么?.(二)师生互动,课堂探究前面我们学习了角平分线的性质,有了这些性质,很多问题不需要证明三角形全等而直接应用性质,因而对解题带来了很大的便利。那么,线段的垂直平分线是否也有一些性质,而这些性质同样方便我们解题呢?这就是我们这节课所要探究的,即线段的垂直平分线的性质。问题3:类比角平分线的性质1,你们能否说出线段的垂直平分线的类似性质以及符号语言表述呢?内容:线段的垂直平分线垂直于这条线段,且平分这条线段。符号语言表述为:∵MN是线段AB的垂直平分线∴MN⊥AB且AO=BO作用:(1)可得垂直(2)可得线段相等类比角平分线的性质2,你能否说出线段的垂直平分线的类似性质以及符号语言表述呢?这似乎有些难度,但我们可以借鉴角平分线性质2的探究过程来探究线段的垂直平分线的性质2.问题4:角平分线性质2的探究过程有哪几步?做一做:同学们照下面的步骤做一做并完成表格:(1)在一张白纸上任意画一条线段AB,对折AB,使点A,点B重合,折痕与线段AB的交点为点O[如图1];(2)在折痕上任取一点,量一量点到点A与点B的距离[如图2];(3)在折痕上另取点,点…,分别量一量点,点…到点A与点B的距离[如图3].1ONMBA想一想:问题5:(1)线段A与线段B,它们有何数量关系?线段A与线段B呢?线段A与线段B呢?(2)O与线段AB有什么特殊关系?(3)你有什么发现?我们只是取了有限的几个点,其它的点是否也有此结论呢?下面大家一起来看一段演示.猜一猜:问题6:由此我们可以猜想出什么结论呢?问题7:不论是同学们动手选取的这几个点还是演示的线段的垂直平分线上的一部分线段上的点,点的选取都是有限的,毕竟线段的垂直平分线是直线,它上面有无数个点,我们不可能一一去测量.但我们光从这有限个数据当中得出这个猜想的正确性,显然理由不够充分,何况实际操作过程中还存在着误差,那我们该如何验证这个猜想呢?问题8:证明一个命题的基本步骤是什么?证一证:线段的垂直平分线上的点与这条线段两个端点的距离相等。(三)归纳和总结由此,我们可以得出线段的垂直平分线的性质是:线段的垂直平分线上的点与这条线段两个端点的距离相等.对于线段的垂直平分线这一性质,我们该如何用符号语言去表述呢?符号语言表述为:∵PO⊥AB且A0=BO∴AP=BP作用:可得共端点的线段相等练一练:1.如图4,NM是线段AB的垂直平分线,点D是MN与线段AB的交点,下列说法正确的有:2.①AB⊥MN,②AD=DB,③MN⊥AB,④MD=DN,⑤AB是MN的垂直平分线.图4图52.如图5,在△ABC中,BC=10,BD=8,DE⊥BC,E为BC的中点,则△BCD的周长是.(四)解决问题例:如图6,在四边形ABCD中,AD∥BC,对角线AC的中点为O,过点O作AC的垂线分别与AD,BC相交于点E,F,连接AF.求证:AE=AF.图63备选题:1.如图7,在△ABC中,BD是∠ABC的平分线,∠A=90°,线段BC的垂直平分线交线段BC于点E,交边AC于点D,且BE=8,BD+DE=a,则S△ABC=.(用含a的代数式表示)2.如图8,点P是∠AOB内一点,点P1,点P2分别是点P关于OA,OB的对称点,线段P1P2交OA于点M,交OB于点N,若P1P2=5cm,则△PMN的周长是.图7图8图93.如图9,点P为ΔABC两边AC,BC的垂直平分的交点,连接AP,BP,CP,∠PAC=40°,∠PCB=30°则∠PBA=,∠BAC=,线段PA,PB,PC的大小关系是.4.如图10,在ΔABC中,AD平分∠BAC,DE是BC的中垂线,E为垂足,过D作DM⊥AB,DN⊥AC交AC的延长线于N。求证:(1)MB=NC(2)图104EDCBA(五)小结:本节课你有什么收获?(六)作业:练习册练习册(七)板书:(八)反思:5