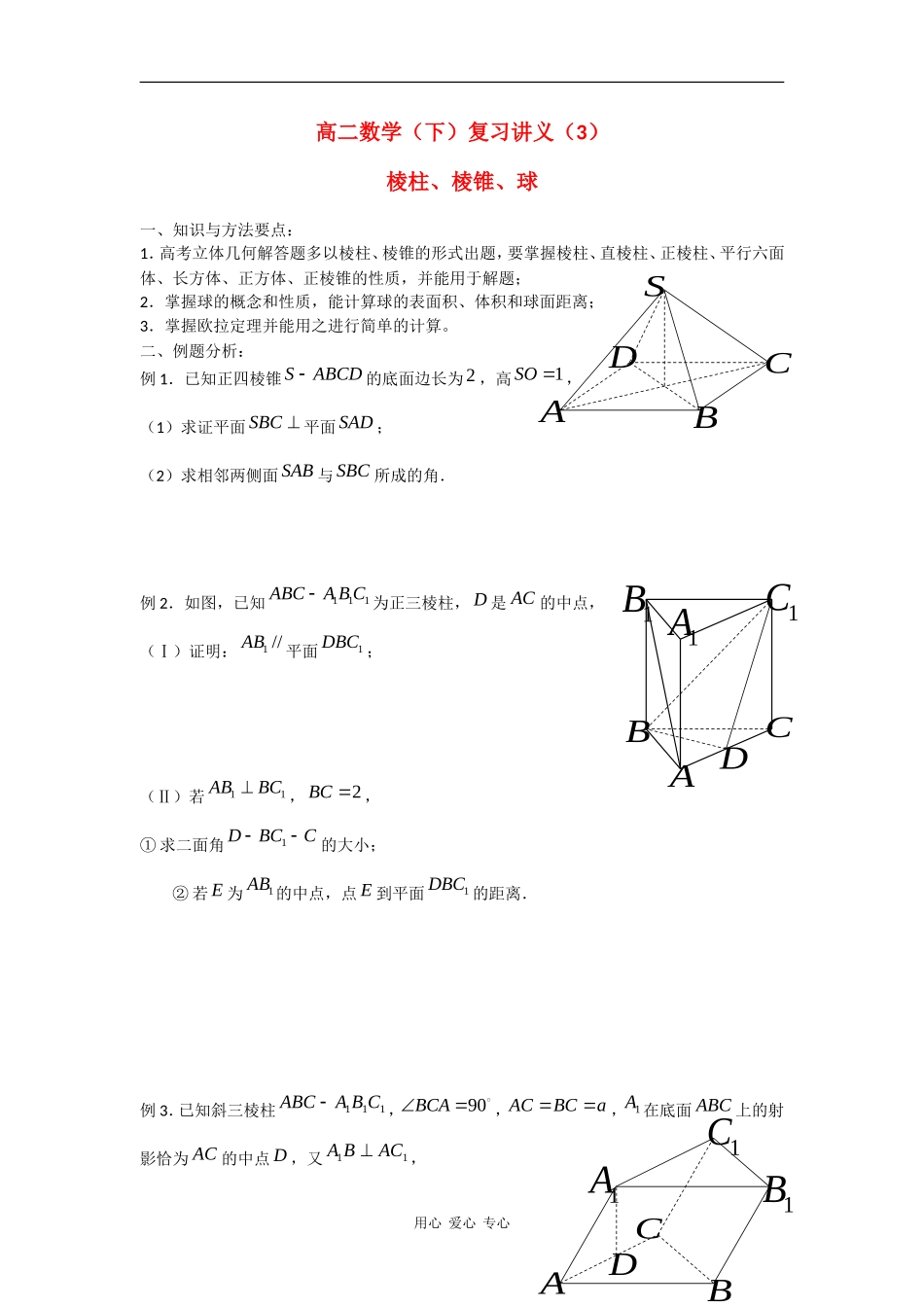
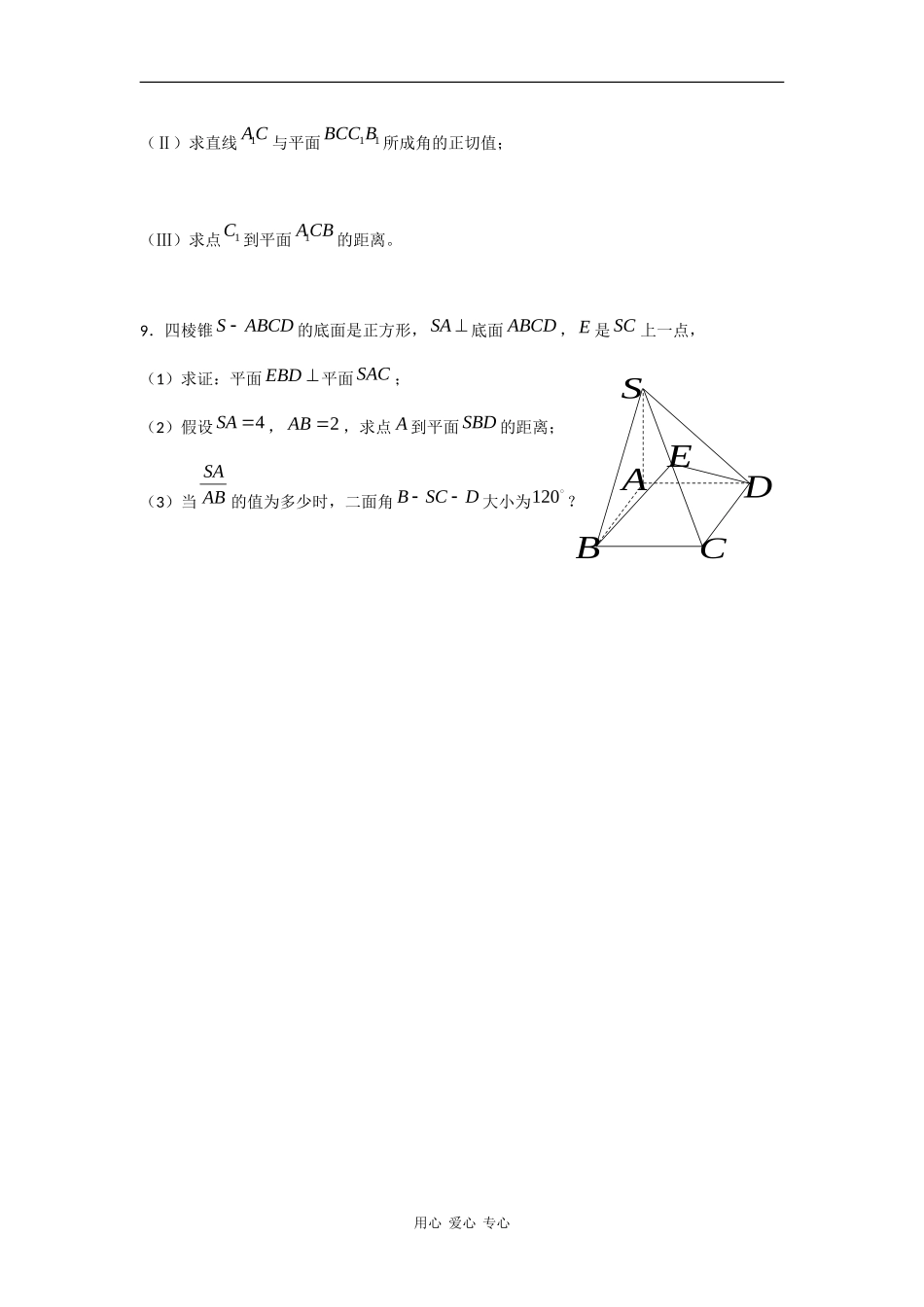
SABCDA1AB1BC1CDABC1A1B1CD高二数学(下)复习讲义(3)棱柱、棱锥、球一、知识与方法要点:1.高考立体几何解答题多以棱柱、棱锥的形式出题,要掌握棱柱、直棱柱、正棱柱、平行六面体、长方体、正方体、正棱锥的性质,并能用于解题;2.掌握球的概念和性质,能计算球的表面积、体积和球面距离;3.掌握欧拉定理并能用之进行简单的计算。二、例题分析:例1.已知正四棱锥SABCD的底面边长为2,高1SO,(1)求证平面SBC平面SAD;(2)求相邻两侧面SAB与SBC所成的角.例2.如图,已知111ABCABC为正三棱柱,D是AC的中点,(Ⅰ)证明:1//AB平面1DBC;(Ⅱ)若11ABBC,2BC,①求二面角1DBCC的大小;②若E为1AB的中点,点E到平面1DBC的距离.例3.已知斜三棱柱111CBAABC,90BCA,ACBCa,1A在底面ABC上的射影恰为AC的中点D,又11ACBA,用心爱心专心(1)求证:BC平面11AACC;(2)求点1A到AB的距离;(3)求二面角1BAAC的正切值。三、课后作业:1.设地球半径为R,在北纬45圈上有甲、乙两地,已知两地间的球面距离为3R,则此两地间的经度差为.2.已知半径1的球面上三点,,ABC,每两点之间的球面距离都是2,那么过,,ABC的截面与球心的距离是.3.下列各图中,是正方体的表面展开图的共有()()A1个()B2个()C3个()D4个4.一个12面体共有8个顶点,其中2个顶点处各有6条棱,其它的顶点处都有相同数目的棱,则其它顶点处各有条棱。5.已知铜的单晶的外形是简单多面体,它有三角形和八边形两种晶面,如果铜的单晶有24个顶点,以每个顶点为一端都有三条棱,则单晶铜的三角形晶面有个,八边形晶面有个。6.半径为R的球的任意两个大圆交于两点,这两点间的距离是.7.湖面上浮着一个球,湖水结冰后将球取出,冰上留下一个直径为24cm,深为8cm的空穴,则这个球的表面积为,体积为.8.如图,在三棱柱111ABCABC中,四边形11AABB是菱形,四边形11BCCB是矩形,ABBC,3CB,4AB,160AAB,(Ⅰ)求证:平面1CAB平面11AABB;用心爱心专心ABC1C1A1B(Ⅱ)求直线1AC与平面11BCCB所成角的正切值;(Ⅲ)求点1C到平面1ACB的距离。9.四棱锥SABCD的底面是正方形,SA底面ABCD,E是SC上一点,(1)求证:平面EBD平面SAC;(2)假设4SA,2AB,求点A到平面SBD的距离;(3)当ABSA的值为多少时,二面角BSCD大小为120?用心爱心专心SABCDE