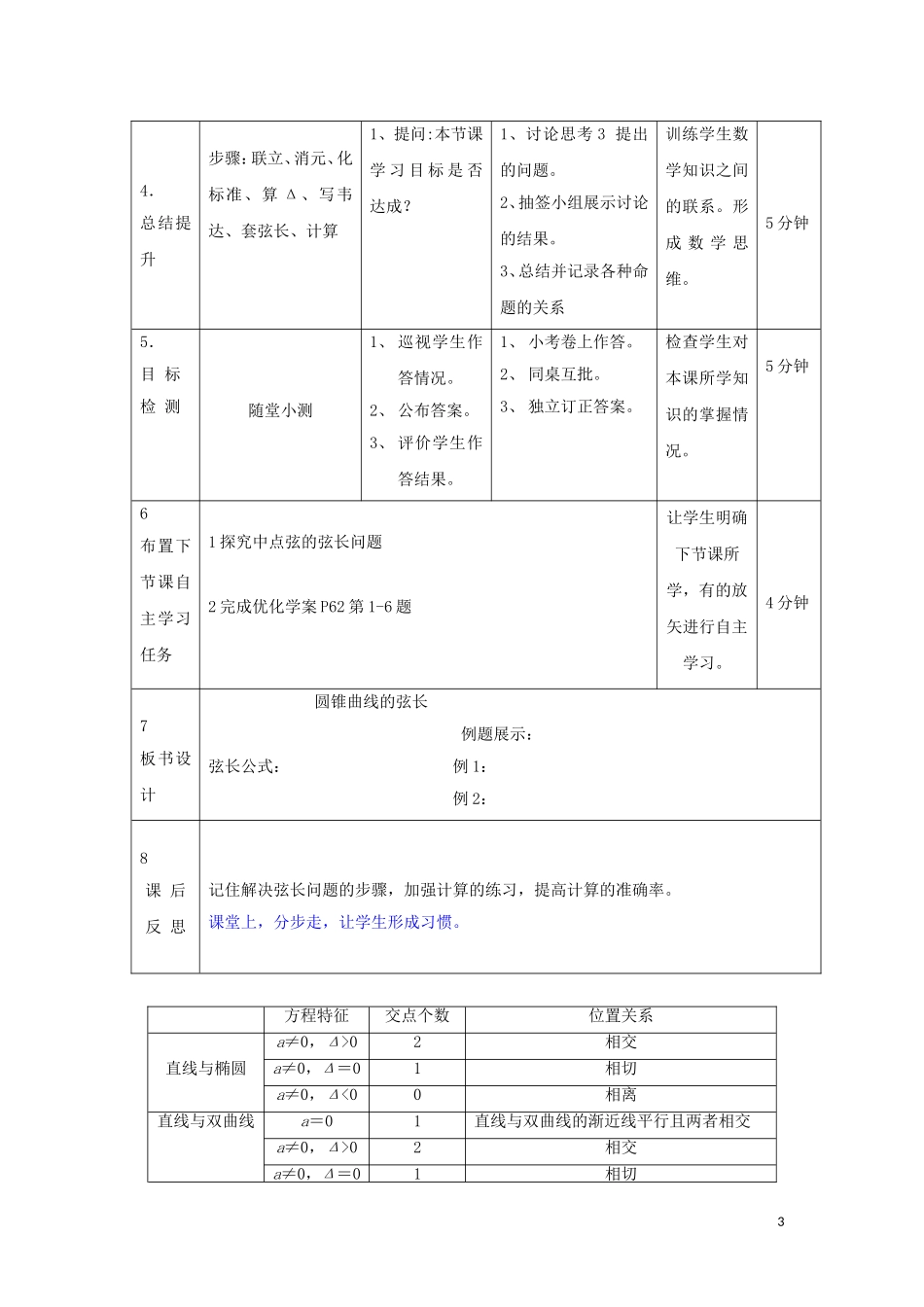
圆锥曲线的弦长课题圆锥曲线的弦长课时第一课时课型新授教学重点求弦长依据:2018年高考大纲分析教学难点正确计算圆锥曲线的弦长依据:学生的计算能力较差积累、归纳总结规律不够。自主学习目标1、在求圆锥曲线弦长的过程中,培养学生严谨的解题态度2、学生牢记弦长公式3、归纳总结求弦长的解题步骤教具多媒体课件、教材,教辅教学环节教学内容教师行为学生行为设计意图时间1.课前3分钟一、小考1、两点间距离公式2、韦达定理3、已知两点求斜率公式二、解读学习目标检查,评价总结小考结果。1.默写公式2.牢记公式明确本节课学习目标,准备学习。3分钟2.承接结果思考1上面三个图直观体验直线与圆锥曲线的位置关系。1、学生自己展示预习习题完成情况。验收学生自主学习的结果,并解决学生自主学习中遇到的困惑。13分钟1象中直线l与椭圆、抛物线、双曲线的图象的位置关系是什么?思考2直线与抛物线、双曲线只有一个公共点时,是否一定相切?弦长公式若直线l:y=kx+b与圆锥曲线交于两点A(x1,y1),B(x2,y2),则弦长2121xxkAB=2122124)(1xxxxk学生从动手实践,再到观察课件,懂得不同条件的轨迹2、小组互相提问。其余学生互相补充并学生对所展示习题进行评价。3、质疑、解答。3.做、议讲、评例1已知直线l:y=2x+m,椭圆C:+=1.试问当m取何值时,直线l与椭圆C:(1)有两个不重合的公共点;(2)有且只有一个公共点;(3)没有公共点?例2:已知双曲线x2-=1,直线l过点P(1,1),当k为何值时,直线l与双曲线C:(1)有一个公共点;(2)有两个公共点;(3)无公共点?1、展示课件2、巡视学生完成情况,让学生更准确的认识命题3、抽查记忆情况。1、学生先独立完成例题,然后以小组为单位统一答案。2、小组讨论并展示自己组所写的过程3、其他组给予评价(主要是找错,纠错)通过具体说写,记住方程。在具体问题中,记住弦长公式,挖掘内在规律、发现数学的本质。3分钟10分钟24.总结提升步骤:联立、消元、化标准、算Δ、写韦达、套弦长、计算1、提问:本节课学习目标是否达成?1、讨论思考3提出的问题。2、抽签小组展示讨论的结果。3、总结并记录各种命题的关系训练学生数学知识之间的联系。形成数学思维。5分钟5.目标检测随堂小测1、巡视学生作答情况。2、公布答案。3、评价学生作答结果。1、小考卷上作答。2、同桌互批。3、独立订正答案。检查学生对本课所学知识的掌握情况。5分钟6布置下节课自主学习任务1探究中点弦的弦长问题2完成优化学案P62第1-6题让学生明确下节课所学,有的放矢进行自主学习。4分钟7板书设计圆锥曲线的弦长例题展示:弦长公式:例1:例2:8课后反思记住解决弦长问题的步骤,加强计算的练习,提高计算的准确率。课堂上,分步走,让学生形成习惯。方程特征交点个数位置关系直线与椭圆a≠0,Δ>02相交a≠0,Δ=01相切a≠0,Δ<00相离直线与双曲线a=01直线与双曲线的渐近线平行且两者相交a≠0,Δ>02相交a≠0,Δ=01相切3a≠0,Δ<00相离直线与抛物线a=01直线与抛物线的对称轴重合或平行且两者相交a≠0,Δ>02相交a≠0,Δ=01相切a≠0,Δ<00相离目标检测:1.若直线y=kx+1与椭圆+=1总有公共点,则m的取值范围是()A.m>1B.m≥1或0a>0),求点P的轨迹.4