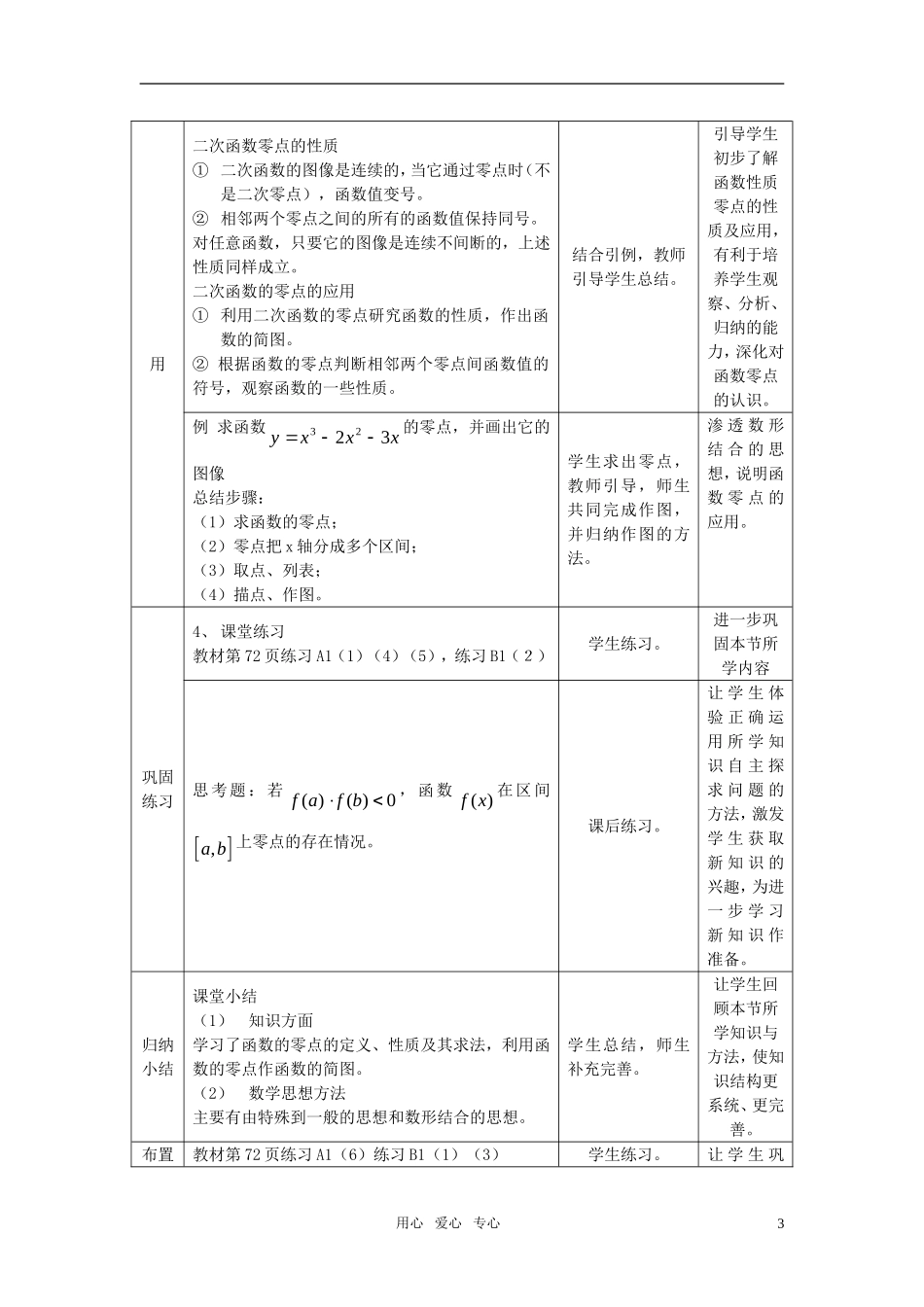
函数的零点一、教学目标1、知识与技能:(1)理解函数零点的意义,会求函数的零点。(2)能判断二次函数零点的存在性,了解函数的零点与方程的关系,初步形成用函数的观点处理问题的意识。2、过程与方法:(1)以具体的二次函数为例,求出零点,并通过作图加以说明,从而给出函数零点的概念,体会由特殊到一般的思维方法。(2)通过由零点的性质作函数图像的过程及函数零点的性质的总结,渗透数形结合的思想方法。3、情感、态度与价值观:让学生初步体会事物间相互转化的辩证思想。一、教学重点、难点教学重点:函数零点的概念、求法及性质;教学难点:函数零点的应用。二、教学方法本节课是对初中内容的加深,学生对相关知识比较熟悉,因此采用以学生活动为主体,自主探究,合作交流的教学方法。四、教学过程教学环节教学内容师生互动设计意图复习引入(1)一元二次方程是否有实根的判定方法(2)二次函数2yaxbxc的顶点坐标、对称轴方程等相关内容。学生思考后回答以旧引新,利于学生构建知识网络。为函数的零点判定及其应用作出铺垫。函数零点的概念1、实例引入例1:已知函数26yxx,(1)当x取何值时,0?y(2)作出函数的简图。2x或3x是函数26yxx的零点。问题一:观察函数的零点在其图像上的位置。学生动手解题,并观察思考,教师总结引例。让学生感知知识发展的过程,了解函数零点与方程根的关系,渗透数形结合的思想。2、函数的零点一般地,如果函数()yfx在实数a处的值等于零,即()0fa,则a叫做这个函数的零点问题二:结合引例给函数的零点下定义。教师提出问题,学生思考回答,师生完培养学生归纳能力,让学生体会由特殊到一般的用心爱心专心1善。思维方法。二次函数零点判定引导学生填写下列表格:一元二次方程二次函数函数图像方程的根图像与x轴交点0322xx322xxy3121xx(-1,0)(3,0)0122xx122xxy21xx=1(1,0)0322xx322xxy无实根没有交点问题三:引导学生填写表格,并思考对于二次函数2yaxbxc如何求函数的零点?是否所有的二次函数都有零点?学生讨论,小组代表发言。体验二次函数零点的各种情形,对一般二次函数零点的总结做出铺垫。3、二次函数零点的判定二次函数2yaxbxc的零点个数,方程20axbxc的实根个数见下表。判别式方程的根函数的零点0两个不相等的实根两个零点0两个相等的实根一个二重零点0无实根无零点师生共同总结,并完成表格。进一步深化学生对函数零点概念的理解。利用表格的形式,有利于学生对比记忆。函数零点性质及应练习:求函数223yxx的零点,并指出0,0yy时,x的取值范围。学生思考、回答。为引出零点的性质作出铺垫用心爱心专心2用二次函数零点的性质①二次函数的图像是连续的,当它通过零点时(不是二次零点),函数值变号。②相邻两个零点之间的所有的函数值保持同号。对任意函数,只要它的图像是连续不间断的,上述性质同样成立。二次函数的零点的应用①利用二次函数的零点研究函数的性质,作出函数的简图。②根据函数的零点判断相邻两个零点间函数值的符号,观察函数的一些性质。结合引例,教师引导学生总结。引导学生初步了解函数性质零点的性质及应用,有利于培养学生观察、分析、归纳的能力,深化对函数零点的认识。例求函数xxxy3223的零点,并画出它的图像总结步骤:(1)求函数的零点;(2)零点把x轴分成多个区间;(3)取点、列表;(4)描点、作图。学生求出零点,教师引导,师生共同完成作图,并归纳作图的方法。渗透数形结合的思想,说明函数零点的应用。巩固练习4、课堂练习教材第72页练习A1(1)(4)(5),练习B1(2)学生练习。进一步巩固本节所学内容思考题:若()()0fafb,函数()fx在区间,ab上零点的存在情况。课后练习。让学生体验正确运用所学知识自主探求问题的方法,激发学生获取新知识的兴趣,为进一步学习新知识作准备。归纳小结课堂小结(1)知识方面学习了函数的零点的定义、性质及其求法,利用函数的零点作函数的简图。(2)数学思想方法主要有由特殊到一般的思想和数形结合的思...