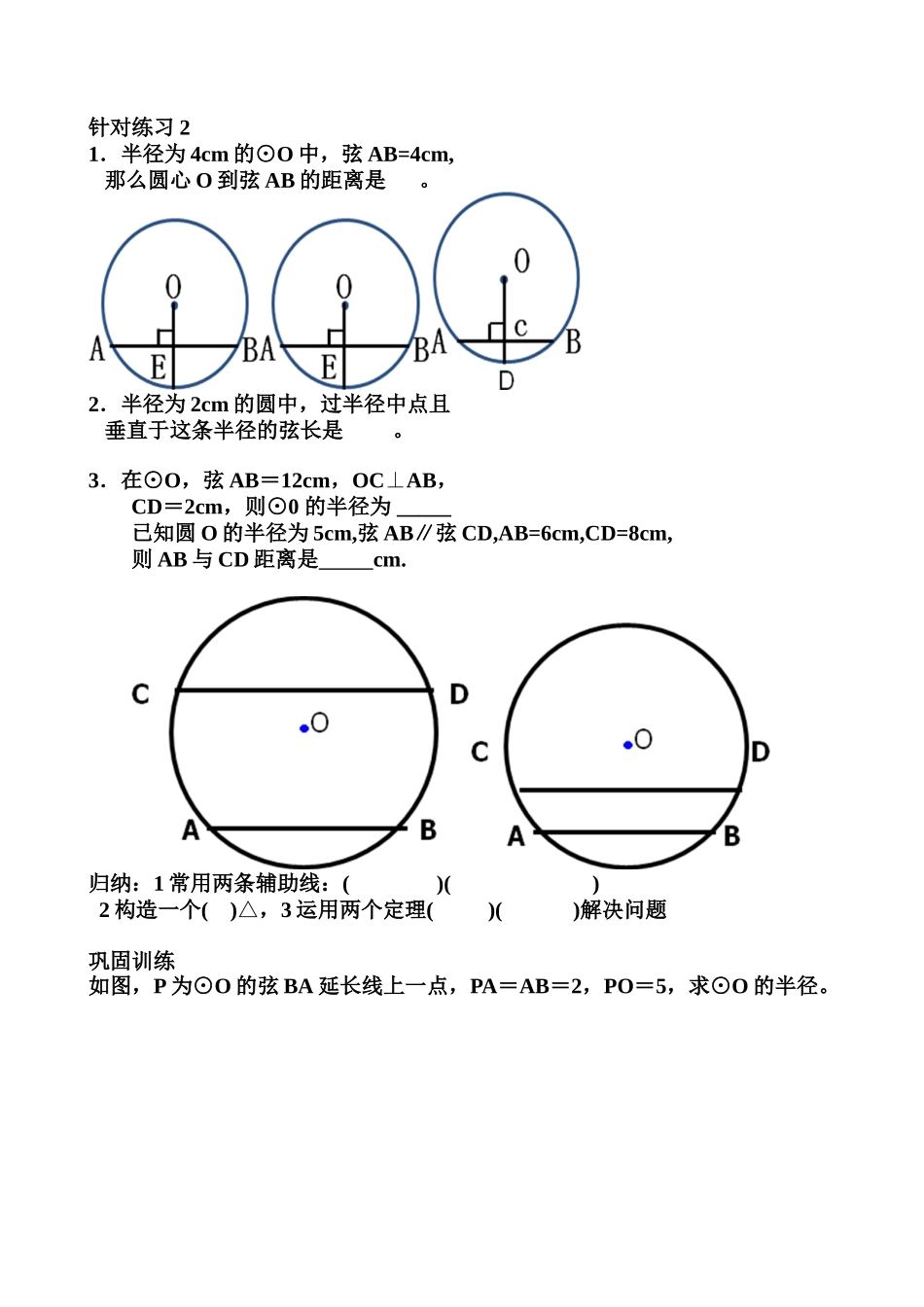
圆的基本性质复习教学设计刘桂花复习目标1、理解圆及其有关概念2.掌握利用垂径定理及推论进行计算和证明的方法3、理解弧、弦、圆心角的关系,圆周角与圆心角的关系4、掌握圆的相关计算和证明重点:圆的基本性质及有关计算难点:辅助线的做法教学过程一、情境示标:(1)情境:由于历年中考考查有关于圆的基本性质的试题总是出现,所以今天我们有必要进行一下这方面知识的复习。(2)示标:出示目标1、理解圆及其有关概念2.掌握垂径定理及推论3.理解弧、弦、圆心角的关系,圆周角与圆心角的关系4.掌握圆的相关计算和证明二、自学指导完成复习提纲内容活动一、小组活动1.组内成员互考概念2.小组探讨概念重要的或容易出错的地方3.完成习题训练4.小组汇报三、交流讲评各小组成员抽签选小组后讲解(一)圆的基本概念:1.圆的定义:到定点的距离等于定长的点的集合叫做圆.2.有关概念:(1)弦、直径(圆中最长的弦)(2)弧、半圆、优弧、劣弧、等弧针对练习1结合图形,找出⊙O中的弦、弧、优弧、劣弧若AB是直径,AB=2DE,∠E=20º,则∠AOC的度数是.BEOACD概念辨析:(1)弦是直径(2)半圆是弧(3)过圆心的线段是直径;(4)半圆是最长的弧;(5)直径是最长的弦;(6)等弧就是长度相等的弧注意-----等弧应同时满足两个条件:1)两弧的长度相等,2)两弧的度数相等。(二)圆的基本性质1.圆的对称性:1)圆是()对称图形,任何()都是它的对称轴.圆有无数条()(2)圆是()对称图形,并且绕()旋转任何一个角度都能与自身重合,即圆具有旋转()2、垂径定理及其推论垂径定理:垂直于弦的直径()弦,并且平分弦所对的()。几何语言:垂径定理推论:平分弦()的直径()于弦,并且平分弦所对的。几何语言:针对练习21.半径为4cm的⊙O中,弦AB=4cm,那么圆心O到弦AB的距离是。2.半径为2cm的圆中,过半径中点且垂直于这条半径的弦长是。3.在⊙O,弦AB=12cm,OCAB⊥,CD=2cm,则⊙0的半径为_____已知圆O的半径为5cm,弦AB∥弦CD,AB=6cm,CD=8cm,则AB与CD距离是cm.归纳:1常用两条辅助线:()()2构造一个()△,3运用两个定理()()解决问题巩固训练如图,P为⊙O的弦BA延长线上一点,PA=AB=2,PO=5,求⊙O的半径。3、圆心角、弧、弦、的关系在同圆或等圆中,如果①两个(),②两条(),③两条()中,有一组量相等,那么它们所对应的其余各组量都分别相等.4.圆周角的性质圆周角定义:定理:一条弧所对的()等于它所对的()的一半.推论:(1)()所对的圆周角相等。(2)直径所对的圆周角是().90°的圆周角所对的弦是().温馨提示(1)在运用圆周角定理时,一定要注意“在同圆或者等圆中”的条件,(2)一条弦对着两条弧,对着两种圆周角且这两种圆周角互补。(3)一条弧只对着一个圆心角,但却对着无数个圆周角。针对练习31、已知∠AOB=120°,求:∠ACB2、已知∠ACD=30°,求:∠AOB3、已知∠AOB=110°,求:∠ACB4.已知在⊙O中,弦AB=1.8cm,∠ACB=30°,则该圆直径等于多少?OCABODBACOBAC5.如图:AB是圆O的直径,BD是圆O的弦,BD到C,AC=AB,BD与CD的大小有什么关系?为什么?BDCAO6、⊙O中,CD⊥AB于点D,点E是弧AB的中点,求证:CE平分∠OCDDEOBAC链接中考:1(2016中考).已知:△ABC内接于⊙O,D是上一点,ODBC⊥,垂足为H.(1)如图1,当圆心O在AB边上时,求证:AC=2OH;(2)如图2,当圆心O在△ABC外部时,连接AD、CD,AD与BC交于点P,求证:∠ACD=APB∠;2、(2017中考)小结:本节课你有什么收获和疑惑?当堂测试小卷板书设计:圆的基本性质复习一、圆的基本概念:例题二、圆的基本性质:例题