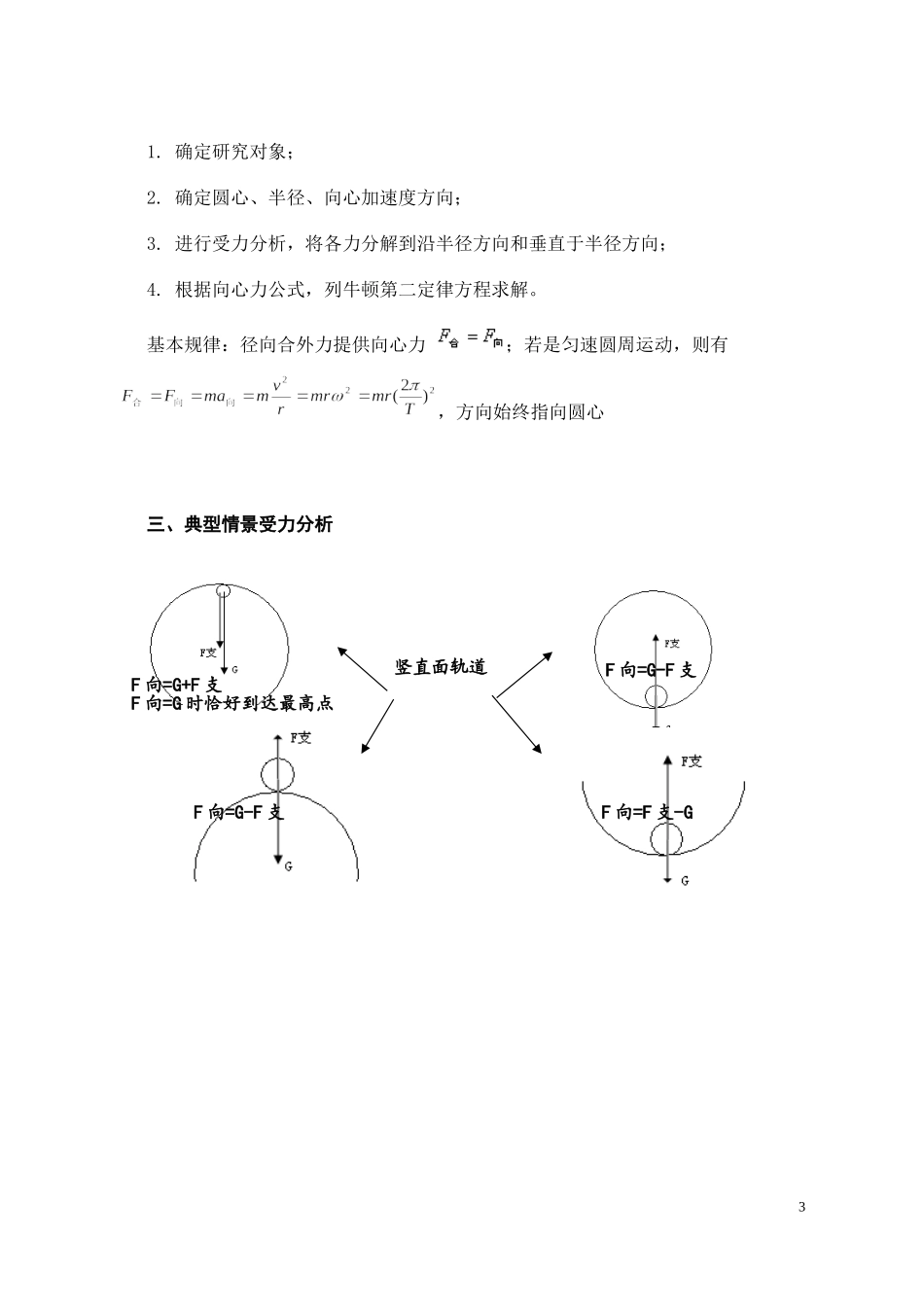
高中圆周运动知识要点、受力分析和题目精讲(复习大全)一、基础知识匀速圆周运动问题是学习的难点,也是高考的热点,同时它又容易和很多知识综合在一起,形成能力性很强的题目,如除力学部分外,电学中“粒子在磁场中的运动”涉及的很多问题仍然要用到匀速圆周运动的知识,对匀速圆周运动的学习可重点从两个方面掌握其特点,首先是匀速圆周运动的运动学规律,其次是其动力学规律,现就各部分涉及的典型问题作点滴说明。匀速圆周运动的加速度、线速度的大小不变,而方向都是时刻变化的,因此匀速圆周运动是典型的变加速曲线运动。为了描述其运动的特殊性,又引入周期(T)、频率(f)、角速度()等物理量,涉及的物理量及公式较多。因此,熟练理解、掌握这些概念、公式,并加以灵活选择运用,是我们学习的重点。1.匀速圆周运动的基本概念和公式(1)线速度大小,方向沿圆周的切线方向,时刻变化;(2)角速度,恒定不变量;(3)周期与频率;(4)向心力,总指向圆心,时刻变化,向心加速度,方向与向心力相同;(5)线速度与角速度的关系为,、、、的关系为。所以在、、中若一个量确定,其余两个量也就确定了,而还和有关。【例1】关于匀速圆周运动,下列说法正确的是()A.线速度不变B.角速度不变C.加速度为零D.周期不变解析:匀速圆周运动的角速度和周期是不变的;线速度的大小不变,但方向时刻变化,故匀速圆周运动的线速度是变化的,加速度不为零,答案为B、D。1【例2】在绕竖直轴匀速转动的圆环上有A、B两点,如图1所示,过A、B的半径与竖直轴的夹角分别为30°和60°,则A、B两点的线速度之比为;向心加速度之比为。解析:A、B两点做圆周运动的半径分别为它们的角速度相同,所以线速度之比加速度之比2.质点做匀速圆周运动的条件(1)具有一定的速度;(2)受到的合力(向心力)大小不变且方向始终与速度方向垂直。合力(向心力)与速度始终在一个确定不变的平面内且一定指向圆心。3.向心力有关说明向心力是一种效果力。任何一个力或者几个力的合力,或者某一个力的某个分力,只要其效果是使物体做圆周运动的,都可以认为是向心力。做匀速圆周运动的物体,所需向心力就是该物体受的合外力,总是指向圆心;而做变速圆周运动的物体,所需向心力则是该物体受的合外力在指向圆心方向的分力,合外力的另一个分力沿着圆周的切线,使速度大小改变,所以向心力不一定是物体所受的合外力。因此,解答圆周运动的基本思路是:先分析物体的受力情况,然后把物体受的各外力沿指向圆心(即沿半径)方向与沿切线方向正交分解,最后用沿指向圆心的合外力等于向心力,即列方程求解做答。二、解决圆周运动问题的步骤21.确定研究对象;2.确定圆心、半径、向心加速度方向;3.进行受力分析,将各力分解到沿半径方向和垂直于半径方向;4.根据向心力公式,列牛顿第二定律方程求解。基本规律:径向合外力提供向心力;若是匀速圆周运动,则有,方向始终指向圆心三、典型情景受力分析竖直面轨道F向=G-F支F向=F支-G3F向=G+F支F向=G时恰好到达最高点F向=G-F支绳(竖直面)F向=F支-GF向=F支+G轻杆F向=F支-GF向=G-F支四、常见问题和处理方法1.皮带传动问题【例3】如图2所示,a、b两轮靠皮带传动,A、B分别为两轮边缘上的点,C与A同在a轮上,已知,,在传动时,皮带不打滑。求:(1);(2);(3)。解析:A、C两点在同一皮带轮上,它们的角速度相等,即,由于皮带不打滑所以A、B两点的线速度大小相等,即。(1)根据知(2)根据知4(3)根据知点评:共轴转动的物体上各点的角速度相同,不打滑的皮带传动的两轮边缘上各点线速度大小相等,这样通过“角速度”或“线速度”将比较“遥远”的两个质点的运动学特点联系在一起。【例4】如图所示,为一皮带传动装置,右轮的半径为r,a是它边缘上的一点,左侧是一轮轴,大轮的半径为4r,小轮的半径为2r,b点在小轮上,到小轮中心的距离为r,c点和d点分别位于小轮和大轮的边缘上,若在传动过程中,皮带不打滑,则()A.a点与b点的线速度大小相等B.a点与b点的角速度大小相等C.a点与c点的线速度大小相等D.a点与d点的向心加速度大小相等解析:皮带不打滑,故a、c两点线...