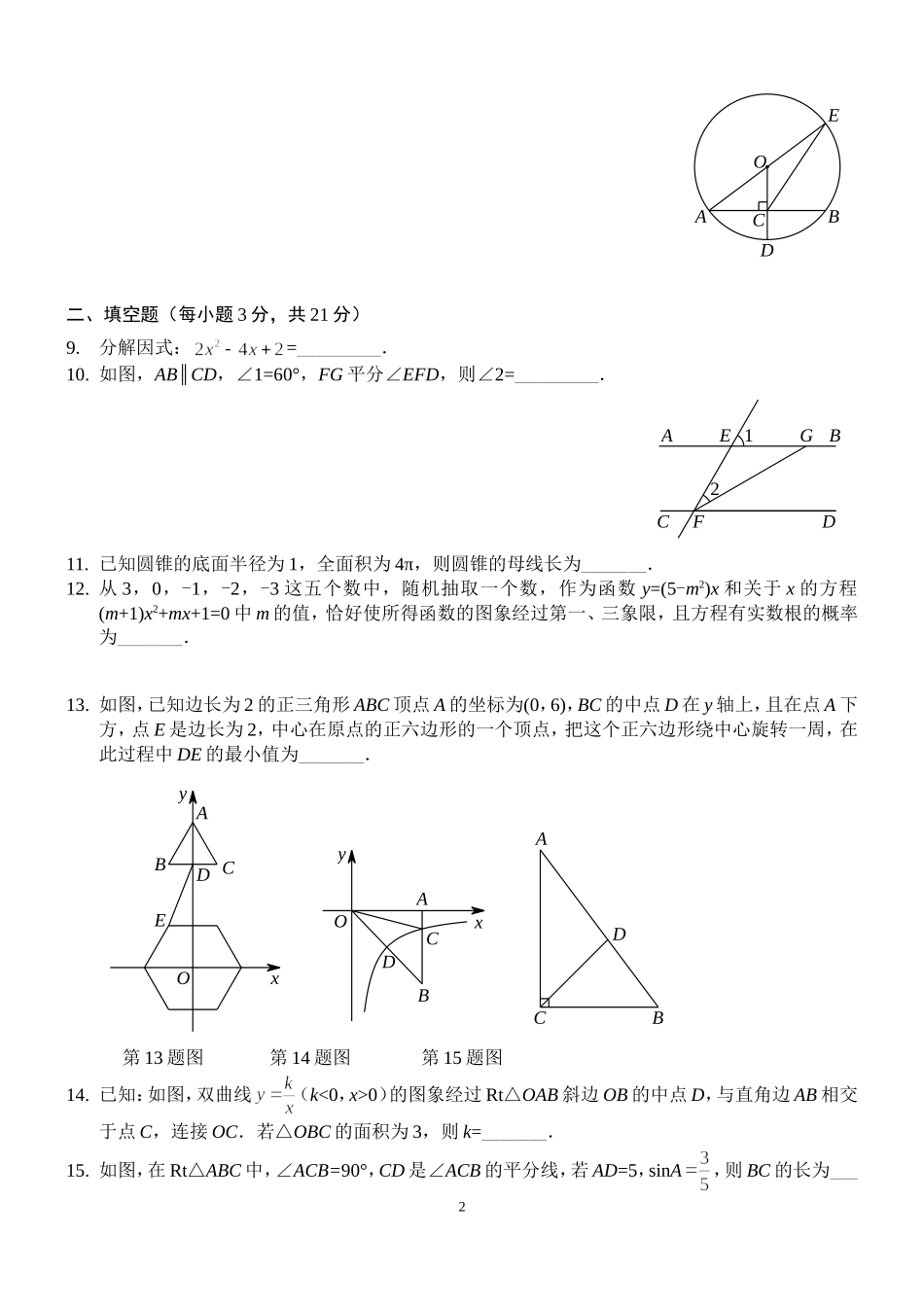
2014年中考数学模拟试卷(二)一、选择题(每小题3分,共24分)1.下列各组数中,互为相反数的是【】A.2和-2B.-2和C.-2和D.和22.不等式4-3x≥2x-6的非负整数解有【】A.1个B.2个C.3个D.4个3.国家统计局公布2013年中国国内生产总值568845亿元,同比增长7.7%,完成了年初设定的7.5%的目标.请你以亿元为单位用科学记数法表示2013年我国的国内生产总值为(结果保留两个有效数字)【】A.5.6×1013B.5.7×1013C.5.7×105D.5.6×1054.如图是一个长方体包装盒,则它的平面展开图可能是【】A.B.C.D.5.已知抛一枚均匀硬币正面朝上的概率为,下列说法错误的是【】A.连续抛一均匀硬币2次必有1次正面朝上B.连续抛一均匀硬币10次都可能是正面朝上C.大量反复抛一均匀硬币,平均100次出现正面朝上50次D.通过抛一均匀硬币确定谁先发球的比赛规则是公平的6.如果将抛物线向右平移1个单位,那么所得新抛物线的表达式是【】A.B.C.D.7.如图,把图1中的△ABC经过一定的变换得到图2中的△A′B′C′,如果图1中△ABC上点P的坐标为(a,b),那么这个点在图2中的对应点P′的坐标为【】A.(a-2,b-3)B.(a-3,b-2)C.(a+3,b+2)D.(a+2,b+3)图1123-1-2-3-3-2-1321POyAxCB图2123-1-2-3-3-2-1321B'A'P'C'Oyx8.如图,⊙O的半径OD⊥弦AB于点C,连接AO并延长,交⊙O于点E,连接CE.若AB=8,CD=2,则CE的长为【】A.B.C.D.1EDCBAO二、填空题(每小题3分,共21分)9.分解因式:=_________.10.如图,AB∥CD,∠1=60°,FG平分∠EFD,则∠2=_________.21GCBADEF11.已知圆锥的底面半径为1,全面积为4π,则圆锥的母线长为_______.12.从3,0,-1,-2,-3这五个数中,随机抽取一个数,作为函数y=(5-m2)x和关于x的方程(m+1)x2+mx+1=0中m的值,恰好使所得函数的图象经过第一、三象限,且方程有实数根的概率为_______.13.如图,已知边长为2的正三角形ABC顶点A的坐标为(0,6),BC的中点D在y轴上,且在点A下方,点E是边长为2,中心在原点的正六边形的一个顶点,把这个正六边形绕中心旋转一周,在此过程中DE的最小值为_______.DxOABECyxyABCDOBCAD第13题图第14题图第15题图14.已知:如图,双曲线(k<0,x>0)的图象经过Rt△OAB斜边OB的中点D,与直角边AB相交于点C,连接OC.若△OBC的面积为3,则k=_______.15.如图,在Rt△ABC中,∠ACB=90°,CD是∠ACB的平分线,若AD=5,sinA,则BC的长为___2____.三、解答题(本大题共8小题,满分75分)16.(8分)(1)计算:;(2)解方程:(2x-1)2=x(3x+2)-7.17.(9分)如图,CD=CA,∠1=∠2,CE=CB.求证:DE=AB.21BEADC18.(9分)在某市中小学生“我的中国梦”读书活动中,某校对部分学生做了一次主题为“我最喜爱的图书”的调查活动,将图书分为甲、乙、丙、丁四类,学生可根据自己的爱好任选其中一类.学校根据调查情况进行了统计,并绘制了不完整的条形统计图和扇形统计图.甲乙丙丁20%40658010080604020丁丙乙甲类别人数请你结合图中信息,解答下列问题:(1)本次共调查了_______名学生,其中,最喜爱甲类图书的人数占本次被调查人数的_______%(2)求被调查的学生中最喜爱丁类图书的学生人数,并补全条形统计图;(3)在最喜爱丙类图书的学生中,女生人数是男生人数的1.5倍,若这所学校共有学生1500人,请你估计该校最喜爱丙类图书的女生和男生分别有多少人?19.(9分)某地下车库出口处“两段式栏杆”如图1所示,点A是栏杆转动的支点,点E是栏杆两段的连接点.当车辆经过时,栏杆AEF升起后的位置如图2所示,其中AB⊥BC,EF∥BC,∠EAB=143°,AB=AE=1.2米,求当车辆经过时,栏杆EF段距离地面的高度(即直线EF上任意一点到直线BC的距离).(结果精确到0.1米,栏杆宽度忽略不计;参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75.)3图1FBCADE图2CBAEFD20.(9分)如图,一次函数的图象经过两点,与反比例函数的图象在第一象限内的交点为M,若△OBM的面积为2.(1)求一次函数和反比例函数的表达式.(2)在y轴上是否存在点P,使得△AMP为等腰三角形?若存在,求出点P的坐标;若不存在,说明理由.MBAyOx21.(10分)为了抓住文化艺术节的商...