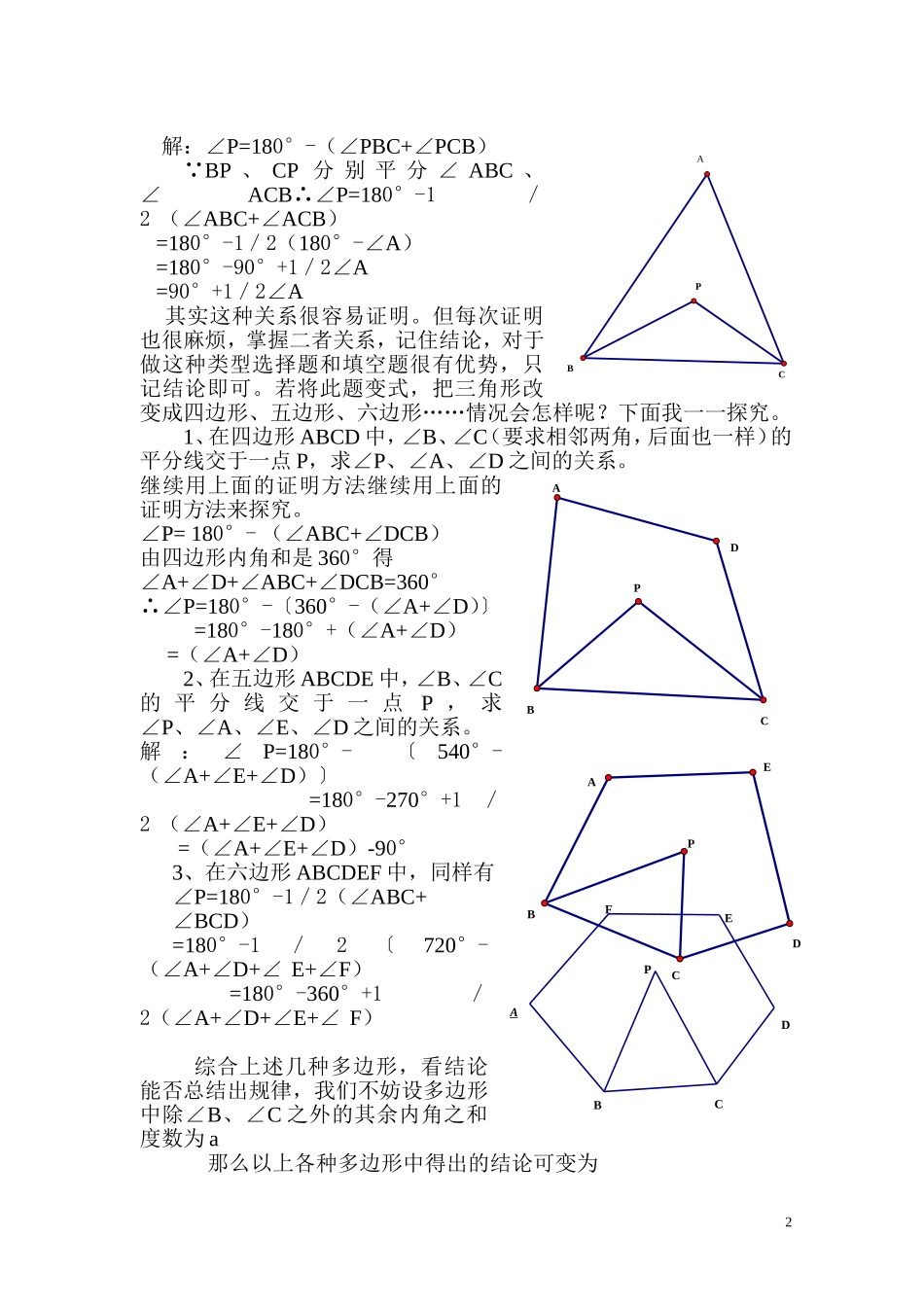
数学专题报告单位:白茆中心校教师:贾海进多边形的两内角平分线的夹角与其它内角的关系专题讨论白茆中心校贾海进有这样一道常见的数学题:在△ABC中,∠B、∠C的平分线交于一点P,求∠P和∠A的关系。解:∠P=180°-(∠PBC+∠PCB)∵BP、CP分别平分∠ABC、∠ACB∴∠P=180°-1/2(∠ABC+∠ACB)=180°-1/2(180°-∠A)=180°-90°+1/2∠A=90°+1/2∠A其实这种关系很容易证明。但每次证明也很麻烦,掌握二者关系,记住结论,对于做这种类型选择题和填空题很有优势,只记结论即可。若将此题变式,把三角形改变成四边形、五边形、六边形……情况会怎样呢?下面我一一探究。1、在四边形ABCD中,∠B、∠C(要求相邻两角,后面也一样)的平分线交于一点P,求∠P、∠A、∠D之间的关系。继续用上面的证明方法继续用上面的证明方法来探究。∠P=180°-(∠ABC+∠DCB)由四边形内角和是360°得∠A+∠D+∠ABC+∠DCB=360°∴∠P=180°-〔360°-(∠A+∠D)〕=180°-180°+(∠A+∠D)=(∠A+∠D)2、在五边形ABCDE中,∠B、∠C的平分线交于一点P,求∠P、∠A、∠E、∠D之间的关系。解:∠P=180°-〔540°-(∠A+∠E+∠D)〕=180°-270°+1/2(∠A+∠E+∠D)=(∠A+∠E+∠D)-90°3、在六边形ABCDEF中,同样有∠P=180°-1/2(∠ABC+∠BCD)=180°-1/2〔720°-(∠A+∠D+∠E+∠F)=180°-360°+1/2(∠A+∠D+∠E+∠F)综合上述几种多边形,看结论能否总结出规律,我们不妨设多边形中除∠B、∠C之外的其余内角之和度数为a那么以上各种多边形中得出的结论可变为2PDCBAPCBAPFEDCBAPEDCBA三角形:∠P=90°+1/2a=1/2a-(-1)×90°四边形:∠P=1/2a=1/2a-0×90°五边形:∠P=1/2a-90°=1/2a-1×90°六边形:∠P=1/2a-180°=1/2a-2×90°……n边形:∠P=1/2a-(n-4)×90°有了上面的规律,我们很方便做类似问题。如在六边形中已知∠B、∠C之和,求∠P或者已知其它四角之和,求∠P,道理一样,直接用结论。其实我们还可以从另一特殊角度来考虑这一题:当这些多边形演变成正多边形时,∠P就变成了正多边形的中心角了,也就=360°/(∠A+∠D),它的度数也就和边数n有关。一般的多边形中的∠P也是和边数n有关,上面的规律即是如此。千变万化的数学中总是能寻求出规律,只要认真观察思考会发现很多有趣的现象,这就是数学的奥妙。3