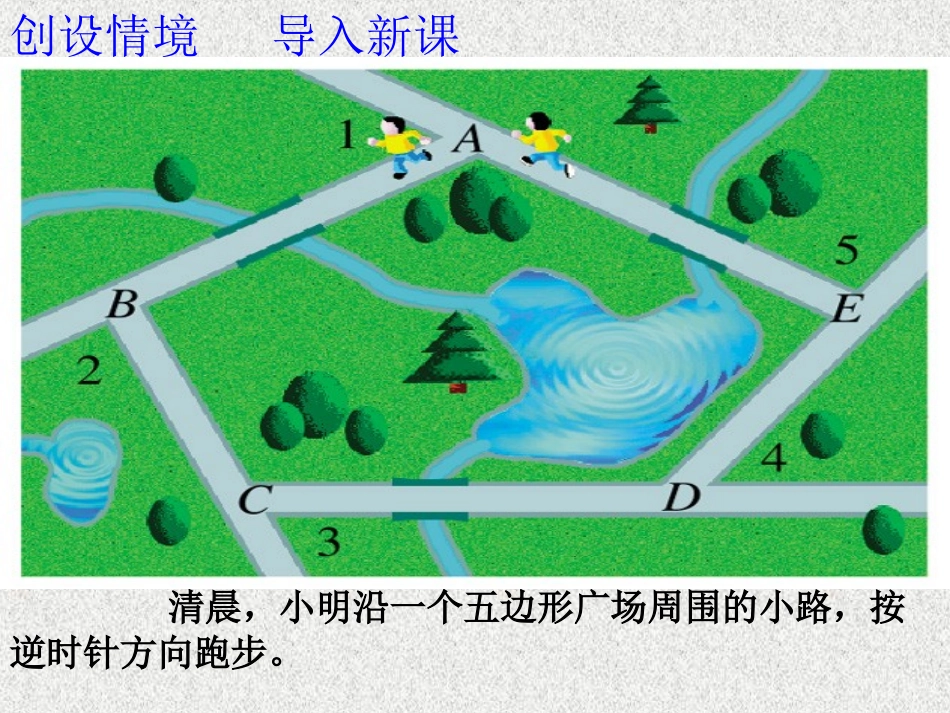
清晨,小明沿一个五边形广场周围的小路,按逆时针方向跑步。创设情境导入新课问题:(1)五边形广场的内角和是多少度?若是正五边形,每个内角是多少度?(2)小明每从一条街道转到下一条街道时,身体转过的角是哪个角?(3)他每跑完一圈,身体转过的角度之和是多少度?(4)在上图中,你能求出1+2+3+4+5=吗?你是怎样得到的?返回探索多边形的外角和西安市七十二中梁东升ABCDE45123多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角。在每个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和。6合作交流解读探究探究活动一:五边形的外角和ABCDE4512312345结论:1,2,3,4,5的和等于360ْADEBCOABCDE12345推理过程:如图,五边形ABCDE中∠1+2+3+4+5∠∠∠∠=5×180°-(5-2)×180°=360°探究活动一:五边形的外角和整体思路:1.先求5个外角+5个内角的和;2.再减去5个内角的和探究活动二:三边形的外角和整体思路:1.先求3个外角+3个内角的和;2.再减去3个内角的和推理过程:如图,三角形ABC中∠1+2+3∠∠=3×180°-(3-2)×180°=360°ABCDEF213容易看出,4个外角+4个内角=4个平角而4个内角的和是360o,那么四边形的外角和就是4X180o-360o=360o探究活动三:四边形的外角和如果广场的形状是六边形、七边形、八边形甚至是n边形,那么还有类似的结论吗?多边形的外角和定理:多边形的外角和等于360°,与边数无关。合作交流解读探究应用迁移巩固提高例1、一个多边形的内角和等于它的外角和的5倍,它是几边形?例2、已知一个多边形的每个内角都相等,且它的每个内角与外角的比为3︰2,求它的对角线的条数.2、如果一个多边形的每一个外角都等于30。那么这个多边形的边数是______3、若一个多边形的内角和与它的外角和相等,则它是______多边形1、正六边形的每一个外角等于______,每一个内角等于_______基础巩固问题:小明和同学做游戏,规则是从某点向前走20米,左拐300,再向前走20米,再左拐300……,如此下去,问:(1)小明能回到出发点吗?若能回到出发点,小明共走了多少米?(2)如果左拐的角度改为360呢?450呢?你能发现角度的规律吗?综合提升多边形的外角及外角和多边形的外角及外角和的定义;的定义;多边形的外角和等于多边形的外角和等于360°360°;;课时小结课时小结总结反思拓展升华作业分层布置:1、基础题:课本第129---130页随堂练习1、22、提高题:课本第130页知识技能1、2、33、挑战自我:(1)在四边形内角中,最多有多少个锐角?最多有多少个直角?最多有多少个钝角?(2)在n边形内角中,最多有多少个锐角?最多有多少个钝角?知识象一艘船让它载着我们驶向理想的……敬请指导敬请指导