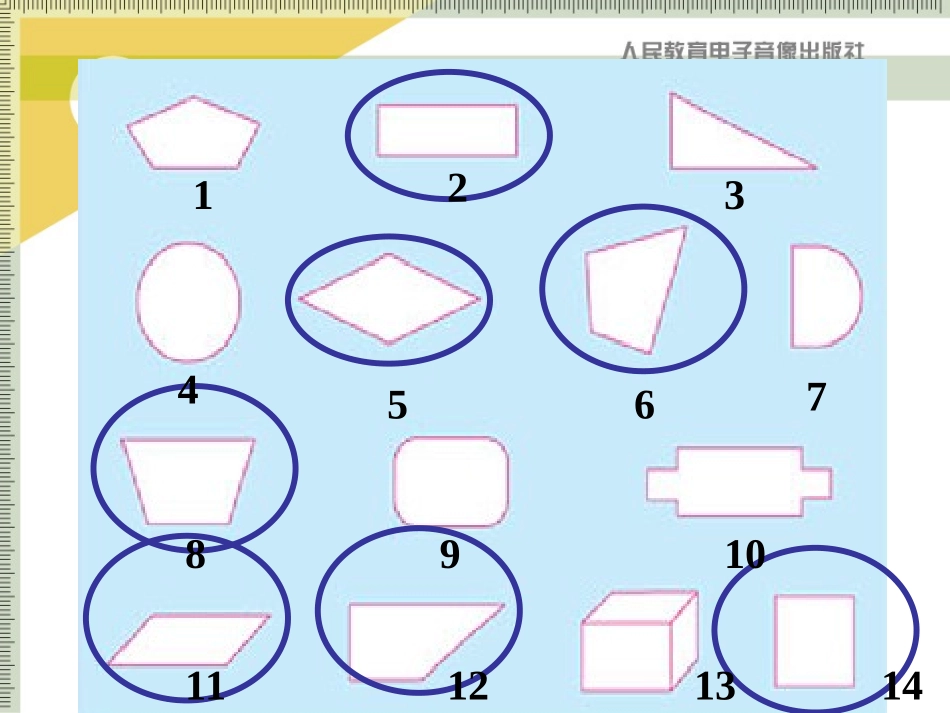
1234567891011121314下面的图片中,有你熟悉的哪些图形?活动11、定义:有两组对边分别平行的四边形叫做平行四边形。3、记作:5、几何语言:2、两要素:ABDC平行四边形的定义:四边形ABCD是平行四边形ABCD两组对边分别平行四边形ABCD∥ADBC∥4、读作:平行四边形ABCD你能从以下图形中找出平行四边形吗?两组对边分别平行,是平行四边形的一个主要特征。23145如图,DC∥EF∥AB,DA∥GH∥CB,图中的平行四边形有__个,它们是_______________________________________________。9AHOEABCDBHGCAHGDCDEFABFECFOGDEOGBHOFDABCOHEFGA.5个B.7个C.9个D.11个1、根据定义画一个平行四边形.探究平行四边形的性质观察你所画的平行四边形,它的边、角之间有什么关系?探究平行四边形的性质请用直尺,量角器等工具度量你所画的平行四边形的边和角,并记录下数据,验证你的猜想是否正确?探究平行四边形的性质探究平行四边形的性质ADCB证明:连接AC1234已知:四边形已知:四边形ABCDABCD是平行四边形是平行四边形求证:求证:AD=BCAB=DCAD=BCAB=DC∠∠BAD=BCDB=D∠∠∠BAD=BCDB=D∠∠∠//ABCD//ADBC1234同理,∠BAC=∠BCD12,34ACCA,,,ABCDBCDABD∵((((在△ABC和△CDA中∴△ABC≌CDA△(ASA)四边形ABCD是平行四边形ADCB平行四边形的邻角互补.平行四边形的邻角互补.平行四边形的性质平行四边形的性质11:平行四边形的对边相等:平行四边形的对边相等平行四边形的性质平行四边形的性质22:平行四边形的对角相等:平行四边形的对角相等想一想:∠A和∠B是什么关系?∠A+B=180°∠∵四边形ABCD是平行四边形∴AB=CD,AD=BC∵四边形ABCD是平行四边形∴∠A=∠C,B∠=∠D小结:平行四边形的性质是证明线段相等和角相等的重要依据和方法。例例11:在:在ABCDABCD中,已知中,已知∠∠AA=32=32。。,,求其余三个角的度数。求其余三个角的度数。ABCD∵四边形ABCD是平行四边形解:且∠A=32。(已知)∴∠A=C∠=32。,∠B=D∠(平行四边形的对角相等)∠A+B∠=180。(平行四边形的邻角互补)∴∠B=D∠=180。-A∠=180。-32。=148。活动3平行四边形性质的应用例题教学:例题教学:例例22::已知在已知在ABCDABCD中,中,AB=5,BC=3,AB=5,BC=3,求求ABCDABCD的周长。的周长。ABCD解:∵四边形ABCD是平行四边形(已知)∴AB=CD,BC=AD(平行四边形的对边相等)又∵AB=5,BC=3(已知)∴AB=CD=5,BC=AD=3例题教学:例题教学:CCABCDABCD=AB+BC+CD+DA=5+3+5+3=16=AB+BC+CD+DA=5+3+5+3=16∴例例33:如图,小明用一根:如图,小明用一根36m36m长的绳子长的绳子围成了一个平行四边形的场地,其中一条围成了一个平行四边形的场地,其中一条边边ABAB长为长为8m8m,其他三条边各长多少?,其他三条边各长多少?解:∵四边形ABCD是平行四边形BCAD;CDAB8CD36ADCDBCAB又136102ADBCABCD∵AB=8例题教学:例题教学:答:AD和BC为10m,CD为8m。如图,四边形ABCD是平行四边形,则:1)∠D=,∠C=;2)AB=,BC=.58°2832122°3228)58°在□ABCD中,①若∠A=120°,则∠B=____,∠C=____,∠D=______;②若∠B+∠D=120°,则∠A=____,∠B=_____;③若∠C-∠D=120°,则∠A=____,∠B=_____。60120601206015030通过本节课的学习,你有什么收获?11.两组对边分别平行的四边形叫做平行四边形..两组对边分别平行的四边形叫做平行四边形.22.平行四边形的性质:对边平行.平行四边形的性质:对边平行对边相等对边相等对角相等对角相等邻角互补邻角互补33、解决平行四边形的有关问题经常连对角线转、解决平行四边形的有关问题经常连对角线转化为三角形的问题。化为三角形的问题。活动4•必做题:课本84页2,3题•选做题:课本91页6题用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?从拼图可以得到什么启示?小结:平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连结对角线转化为两个全等的三角形进行解题。上图的平行四边形ABCD中有几对全等三角形?BADCO