回归分析的基本思想及初步应用VIP免费

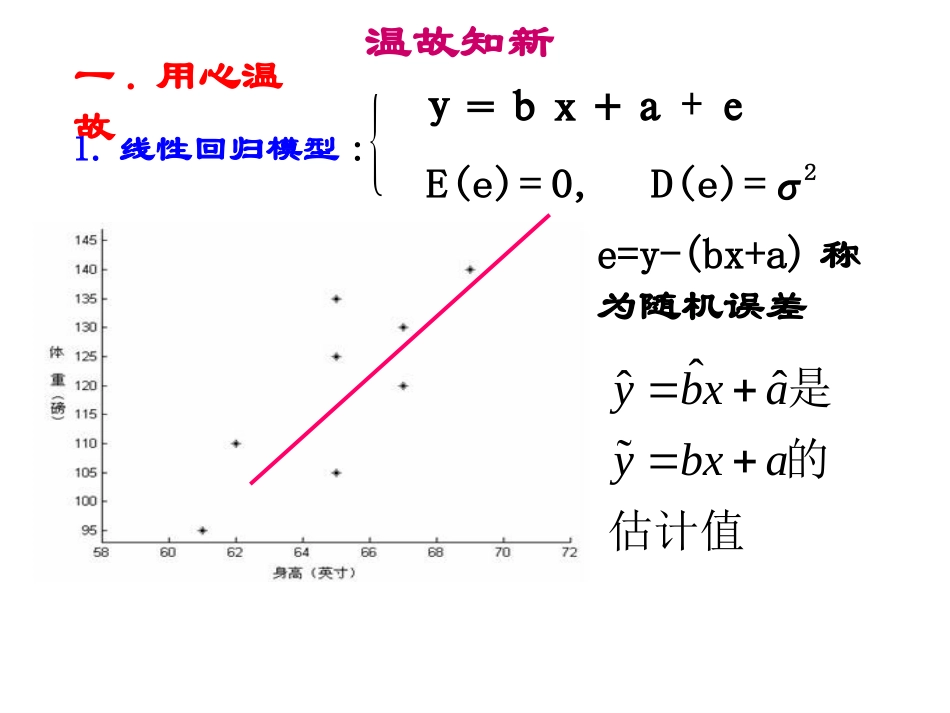
2E(e)=0,D(e)=σｙ＝ｂｘ＋ａ+ｅ1.线性回归模型:ˆˆˆybxaybxa是的估计值e=y-(bx+a)称为随机误差温故知新一.用心温故ˆˆˆ()niiibyy21＝为残差平方和。Q(a,)ˆˆiiieyyii对于样本点（x,y）的随机误差的估计值程称相应残差ˆ.2e残差R2越大模型越好残差平方和越小精确度越高3.相关指数R2n2ii2i=1n2ii=1(y-y)R=1-(y-y)引例:从某大学中随机选出8名女大学生，其身高和体重数据如下表：编号12345678身高165165157170175165155170体重4857505464614359残差(1)求每个点(xi,yi)的残差(2)画出残差的散点图(3)求出相关指数R2,说明身高在多大程度上解释了体重的变化.二.探求新知-6.3732.6272.419-4.6181.1376.627-2.8830.382-8-6-4-22468O21346578910编号残差........③.R2=0.64,表明女大学生的身高解释了64%的体重变化。②残差点比较均匀地落在(以x轴为中心）水平带状区域内.模型较合适带状区域的宽度越窄,模型拟合精度越高,回归方程的预报精度越高.43210-1-2-3-401002003004005006007008009001000454035302520151050-5010203040506070809010025002000150010005000-500-10000102030405060708090100200150100500-50-100-1500102030405060708090100.............................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................（１）分析下列残差图,所选用的回归模型效果最好的是（）牛刀小试（2）有下列说法：①在残差图中，残差点比较均匀地落在水平的带状区域内，说明选用的模型比较合适。②相关指数R2来刻画回归的效果,R2值越大，说明模型的拟合效果越好。③比较两个模型的拟和效果，可以比较残差平方的大小，残差平方和越小的模型，拟合效果越好。正确的是（）①②③建立回归模型的基本步骤画出散点图;确定回归方程类型;求出回归方程;利用相关指数或残差进行分析.确定解释变量和预报变量;被害棉花红铃虫喜高温高湿，适宜各虫态发育的温度为25℃一32℃，相对湿度为80％一100％，低于20℃和高于35℃卵不能孵化，相对湿度60％以下成虫不产卵。冬季月平均气温低于一4．8℃时，红铃虫就不能越冬而被冻死。创设情景1953年，18省发生红铃虫大灾害，受灾面积300万公顷，损失皮棉约二十万吨。因材施教温度xoC21232527293235产卵数y/个711212466115325例2现收集了一只红铃虫的产卵数y和温度xoC之间的7组观测数据列于下表：（1）试建立产卵数y与温度x之间的回归方程；并预测温度为28oC时产卵数目。（2）你所建立的模型中温度在多大程度上解释了产卵数的变化？问题呈现：画散点图假设线性回归方程为：选模型分析和预测当x=28时，y=19.87×28-463.73≈93选变量解：选取气温为解释变量x，产卵数为预报变量y。合作探究050100150200250300350036912151821242730333639方案1当x=28时，y=19.87×28-463.73≈93ˆˆˆybxa估计参数由计算器得：线性回归方程为ˆ19.87463.73yx0残差编号12345671020304050607080-10-20-30-40-50-6090100xy残差21723112521272429663211535325线性模型53.4617.72-12.02-48.76-46.5-57.1193.28ˆ19.87463.73yx271ˆˆˆ(,)()iiiQabyy19818.9相关指数R2≈0.7464所以，一次函数模型中温度解释了74.64%的产卵数变化。y=bx2+a变换y=bx+a非线性关系线性关系方案2问题１选用y=bx2+a，还是y=bx2+cx+a？问题3-200-1000100200300400-40-30-20-10010203040产卵数气温问题2如何求a、b？合作探究t=x2...