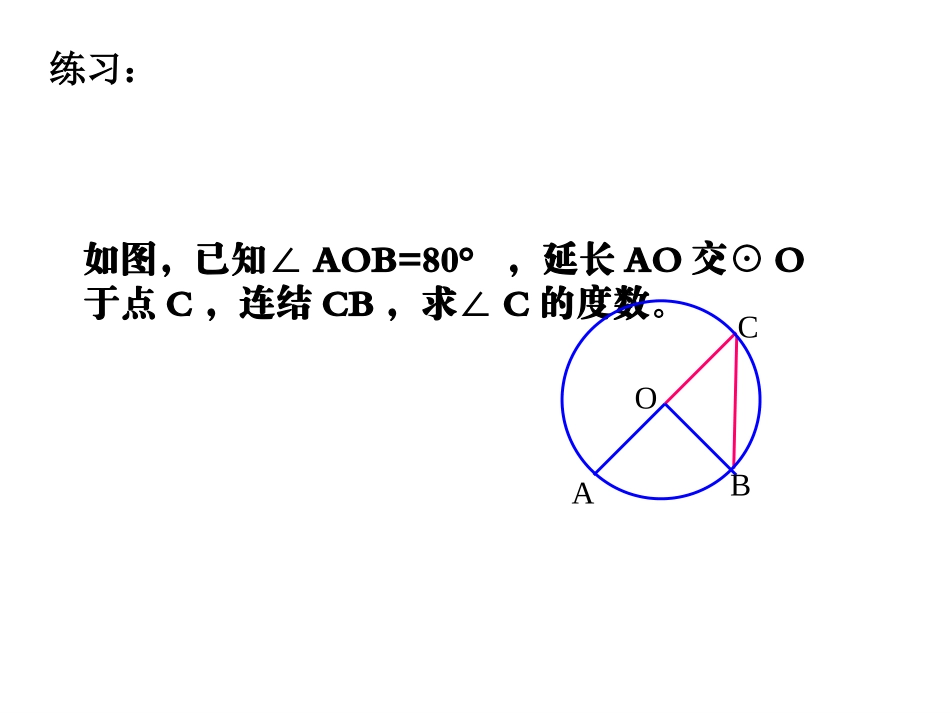
回忆1.什么叫圆心角?.OAB顶点在圆心的角叫圆心角2.圆心角、弧、弦、弦心距四个量之间关系的一个结论,这个结论是什么?在同圆(或等圆)中,如果圆心角、弧、弦、弦心距有一组量相等,那么它们所对应的其余三个量都分别相等。如图,已知∠AOB=80°,延长AO交⊙O于点C,连结CB,求∠C的度数。OABC练习:•当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC,∠ADC,∠AEC.这三个角的大小有什么关系?.BACDEE●OBDCAAC所对角∠AEC∠ABC∠ADC的大小有什么关系?⌒生活实践www.qyxk.net中学数学网(群英学科)收集提供圆周角•当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC,∠ADC,∠AEC.这三个角有何特点?它们的大小有什么关系?.●OBACBACBACBACBACBACBACDEDE顶点在圆上,并且两边都与圆相交的角,叫做圆周角.问题探讨:判断下列图形中所画的∠P是否为圆周角?并说明理由。PPPP不是是不是不是顶点不在圆上。顶点在圆上,两边和圆相交。两边不和圆相交。有一边和圆不相交。圆心角定义:顶点在圆心的角叫圆心角.OBCA圆周角定义:顶点在圆上,并且两边都和圆相交的角叫圆周角.问题3:圆周角概念与圆心角概念在表述上有什么区别?答:圆周角强调角的两边与圆相交,而圆心角不必强调这一点。因为以圆心为顶点的角一定会和圆相交。•当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC,∠ADC,∠AEC.这三个角的大小有什么关系?.BACDEE●OBDCAAC所对角∠AEC∠ABC∠ADC的大小有什么关系?⌒生活实践已知:在⊙O中,弧BC所对的圆周角是∠BAC,圆心角是∠BOC求证:BOCBAC21•结论:在同圆中,一条弧所对的圆周角相等,都等于这条弧所对的圆心角的度数的一半。教师提示:注意圆心与圆周角的位置关系.(1)圆心是圆周角的一条边上,(2)圆心在圆周角的内部,(3)圆心在圆周角的外部.1.第一种情况:ABCO OA=OC∴∠A=C∠又∠BOC=A∠+∠C∴∠BOC=2A∠∠即A=BOC∠21圆周角∠BAC与圆心角∠BOC的大小关系.老师期望:你可要理解并掌握这个模型.ABCOD证明:由第1种情况得∠即BAC=BOC∠21∠BAD=∠BOD21∠CAD=∠COD21∠BAD+∠CAD=∠BOD+∠COD21212.第二种情况:老师提示:能否转化为1的情况?证明:作射线AO交⊙O于D。由第1种情况得∠即BAC=BOC∠21∠BAD=∠BOD21∠CAD=∠COD21∠CAD-∠BAD=∠COD-∠BOD2121ABCOD3.第三种情况:老师提示:能否转化为1的情况?归纳总结在同圆中,同一条弧所对的圆周角相等;都等于这条弧所对的圆心角的一半.·ABCDEO归纳总结在同圆或等圆中,同弧(或等弧)所对的圆周角相等;都等于这条弧所对的圆心角的一半.圆周角定理·ABCDEO思考:在同圆或等圆中,相等的圆周角所对的弧相等吗?在同圆或等圆中,如果两个圆周角相等,它们所对的弧一定相等。ABOC如图,AB是直径,则∠ACB=____90度半圆(或直径)所对的圆周角是直角,90度的圆周角所对的弦是直径。•当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC,∠ADC,∠AEC.这三个角的大小有什么关系?.BACDE生活实践E●OBDCA规律:都相等,都等于圆心角∠AOC的一半AC所对的圆周角∠AEC∠ABC∠ADC的大小有什么关系?⌒结论:同弧或等弧所对的圆周角相等。1、如图,在⊙O中,ABC=50°,则∠AOC等于()A、50°;B、80°;C、90°;D、100°ACBOD2、如图,△ABC是等边三角形,动点P在圆周的劣弧AB上,且不与A、B重合,则∠BPC等于()A、30°;B、60°;C、90°;D、45°CABPB练习练习::3、求圆中角X的度数BAO.70°xAO.X120°练习练习::600BP(1)(2)12003504、如图,△ABC的顶点A、B、C都在⊙O上,∠C=30°,AB=2,则⊙O的半径是。CABO解:连接OA、OB ∠C=30°,∴∠AOB=60°又 OA=OB,∴△AOB是等边三角形∴OA=OB=AB=2,即半径为2。2练习练习::5:已知⊙O中弦AB的等于半径,求弦AB所对的圆心角和圆周角的度数。OAB圆心角为60度圆周角为30度或150度。1.1.圆周角定义圆周角定义::顶点在圆上顶点在圆上,,并且并且两边都和圆两边都和圆相交相交的角叫圆周角的角叫圆周角..3.3.在同圆在同圆((或等圆或等圆))中,同弧或等弧所对的圆周角中,同弧或...