向量法求空间角VIP免费

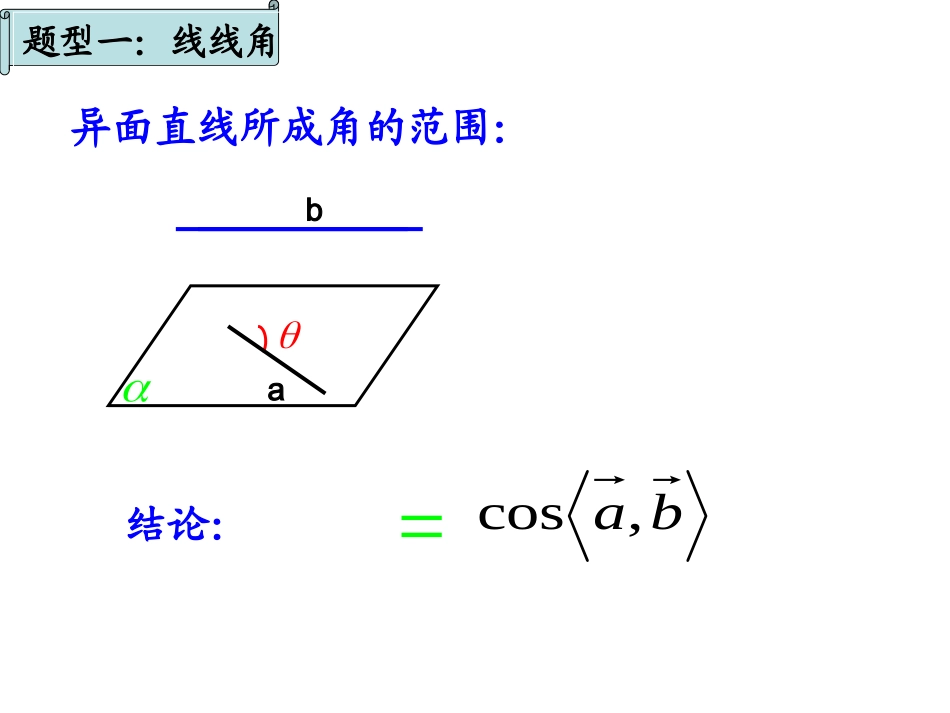
用向量法求空间角哈十二中毕建宏异面直线所成角的范围：0,2题型一：线线角ab结论：cos||ba,cos直线与平面所成角的范围：[0,]2ABO结论：sincos,nAB��||题型二：线面角二面角的范围：[0,]1n�2n�2n�1n�cos12|cos,|nn�ABO12|cos,|nn�cos题型三：二面角.B-DE-A(2)BED;CA13EC.ECCCE4,2ABAAA-ABCD111111111的余弦值求二面角平面）证明：（上且在点中，如图，正四棱柱DCBABCDB1A1D1C1E二面角的范围：[0,]1n�2n�2n�1n�cos12|cos,|nn�ABO关键：根据题意观察二面角的范围12|cos,|nn�cos题型三：二面角第二部分例题分析1、如右图，直三棱柱A1B1C1─ABC中，∠BCA=90°，点D1、E1分别是A1B1、A1C1的中点，若BC=CA=CC1，求直线BD1与AE1所成的角的余弦值.A1C1E1B1D1ABCCxyz),1,21,0(),0,1,0(1EA)1,21,21(),0,0,1(1DB所以：)1,21,0(1AE)1,21,21(1BD1030,coscos111111BDAEBDAEBDAE所以与所成角的余弦值为1BD1AE103011CC解：以C为坐标原点建立空间直角坐标系，设直线则与所成角为1BD1AE,A1C1E1B1D1ABC向量法求异面直线所成角的余弦值的一般步骤：建系求两异面直线的方向向量求两方向向量夹角的余弦值得两异面直线所成角的余弦值2、如图，在长方体AC1中，棱AB=BC=3，棱BB1=4，点E是CC1的中点。求（1）直线ED与平面A1B1C所成角的正弦值.B1BA1D1C1CDEAyzx向量法求直线与平面所成角的正弦值的一般步骤：建系求直线的方向向量求平面的法向量求直线的方向向量与平面的法向量夹角的余弦值得直线与平面所成交的正弦值2、如图，在长方体AC1中，棱AB=BC=3，棱BB1=4，点E是CC1的中点。求（1）直线ED与平面A1B1C所成角的正弦值.B1BA1D1C1CDEA（2）二面角B1A―1CC―1的余弦值。yzxp向量法求二面角的余弦值的一般步骤：建系求两平面的法向量求两法向量夹角的余弦值得二面角的余弦值.,21904的大小求：二面角为直二面角，若二面角到使折起，沿，将，中，、如图，直角梯形DBCABACDDDACADCaABDCADBADDABCDADCBABCDD5、如图，已知：直角梯形OABC中，OA∥BC,∠AOC=90°，SO⊥面OABC，OS=OC=BC=1,OA=2。求：(1)异面直线SA和OB所成的角;OABCS(2)直线OS与平面SAB所成角xyzOABCSyz思考：如图，已知：直角梯形OABC中，OA∥BC,∠AOC=90°，SO⊥面OABC，OS=OC=BC=1OA=2。问：(1)在直线SC上是否存在点D,使得异面直线SA和OD所成的角为;(2)在直线SC上是否存在点D,使得直线OD与面SAB所成角为.x44