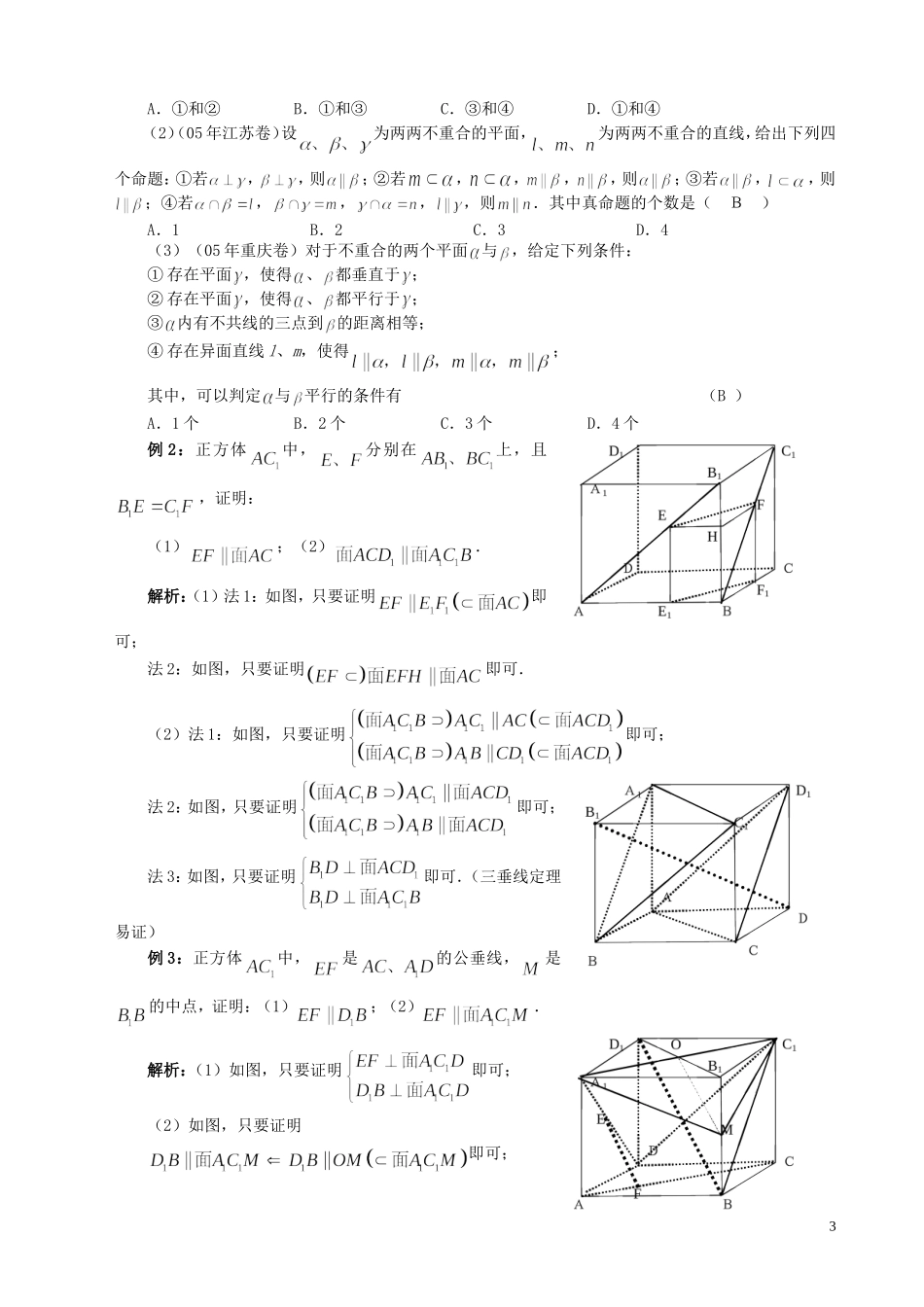
第三讲平行转化术(平行5-3-4)一、考情分析立体几何中的平行关系的证明及应用是高考的重点内容之一,考查内容灵活多样.本节主要帮助考生深刻理解线线平行、线面平行、面面平行的转化术,并能利用它们解决一些问题.二、知识归纳(一)转化框图(二)线线平行的判定方法(1)定义法:同一平面内的不相交的两条直线叫平行直线;推理模式:.(2)公理法:平行于同一条直线的两条直线平行;推理模式:.(3)线面平行的性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行;推理模式:.(4)两个平面平行的性质定理:如果两个平行平面同时和第三个平面相交,那么它们的交线平行;推理模式:.(5)线面垂直的性质:垂直于同一平面的两条直线平行;推理模式:.(三)线面平行的判定方法(1)定义法:一条直线和一个平面没有公共点,称这条线与已知平面平行;推理模式:.1(2)线面平行的判定定理:如果平面外的一条直线和平面内的一条直线平行,那么这条直线和这个平面平行;推理模式:.(3)面面平行的性质:两个平面平行,其中一个平面内的直线必平行于另一个平面;推理模式:.(四)面面平行的线面平行的判定方法(1)定义法:如果两个平面没有公共点,那么这两个平面互相平行;推理模式:.(2)面面平行的判定定理:如果一个平面内有两条相交直线分别平行于另一个平面,那么这两个平面互相平行;推理模式:.(3)面面平行的判定定理的推论:如果一个平面内有两条相交直线分别平行于另一个平面内的两条相交直线,那么这两个平面互相平行;推理模式:.(4)线面垂直的性质:垂直于同一条直线的两条平面平行;推理模式:.三、精典例析例1:(1)(05年辽宁卷)已知是两条不重合的直线,是三个两两不重合的平面,给出下列四个命题:①若,则;②若,则;③若,则;④若是异面直线,,则;其中真命题是(D)2A.①和②B.①和③C.③和④D.①和④(2)(05年江苏卷)设为两两不重合的平面,为两两不重合的直线,给出下列四个命题:①若,,则;②若,,,,则;③若,,则;④若,,,,则.其中真命题的个数是(B)A.1B.2C.3D.4(3)(05年重庆卷)对于不重合的两个平面与,给定下列条件:①存在平面,使得、都垂直于;②存在平面,使得、都平行于;③内有不共线的三点到的距离相等;④存在异面直线l、m,使得;其中,可以判定与平行的条件有(B)A.1个B.2个C.3个D.4个例2:正方体中,分别在上,且,证明:(1);(2).解析:(1)法1:如图,只要证明即可;法2:如图,只要证明即可.(2)法1:如图,只要证明即可;法2:如图,只要证明即可;法3:如图,只要证明即可.(三垂线定理易证)例3:正方体中,是的公垂线,是的中点,证明:(1);(2).解析:(1)如图,只要证明即可;(2)如图,只要证明即可;3例4:如图,截面平行于三棱锥的对棱,(1)证明:截面是平行四边形;(2),截面能否为菱形?(3)截面能否为矩形?正方形呢?(4)若,证明:截面的周长为定值;(5)若,对棱所成的角为,求截面的面积的最大值.解析:(1)只要证明;(2)若截面能否为菱形,则:,故当时,截面为菱形;(3)当时,截面为矩形;当时,截面为正方形;(4)∵,∴截面的周长为(定值);(5)∵,∴截面的面积(当且仅当时,取等号).故当时,截面的面积的取得最大值,且最大值是.四、课后反思4.5