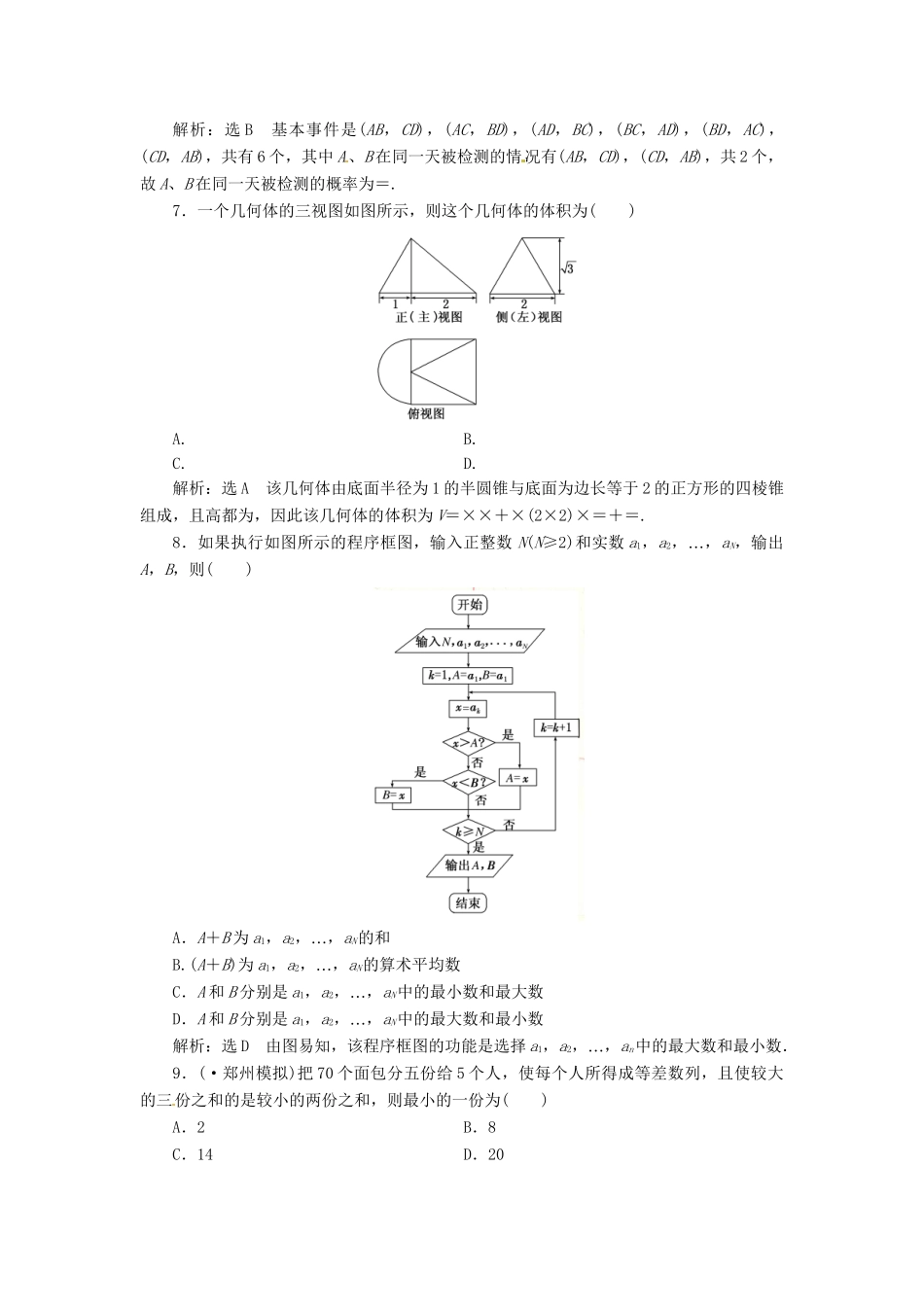
“12+4”提速专练卷(四)一、选择题1.若i为虚数单位,则复数z=5i(3-4i)在复平面内对应的点所在的象限为()A.第一象限B.第二象限C.第三象限D.第四象限解析:选Az=5i(3-4i)=20+15i,则复数对应的点在第一象限.2.已知全集U=R,函数y=的定义域为M,N={x|log2(x-1)<1},则如图所示阴影部分所表示的集合是()A.{x|-2≤x<1}B.{x|-2≤x≤2}C.{x|11025的最小n值是()A.9B.10C.11D.12解析:选C因为a1=1,log2an+1=log2an+1(n∈N*),所以an+1=2an,an=2n-1,Sn=2n-1,则满足Sn>1025的最小n值是11.4.设点M是线段BC的中点,点A在直线BC外,2=16,|+|=|-|,则||=()A.2B.4C.6D.8解析:选A由|+|=|-|,得·=0,所以AM为直角三角形ABC斜边上的中线,所以||=||=2.5.(·合肥模拟)给出命题p:直线l1:ax+3y+1=0与直线l2:2x+(a+1)y+1=0互相平行的充要条件是a=-3;命题q:若平面α内不共线的三点到平面β的距离相等,则α∥β.对以上两个命题,下列结论中正确的是()A“.命题p且q”为真B“.命题p或q”为假C“.命题p或(綈q)”为假D“.命题p且(綈q)”为真解析:选D若直线l1与直线l2平行,则必满足a(a+1)-2×3=0,解得a=-3或a=2,但当a=2时两直线重合,所以l1∥l2⇔a=-3,所以命题p为真.如果这三点不在平面β的同侧,则不能推出α∥β,所以命题q为假.6.中小学校车安全问题引起全社会的强烈关注,为了彻底消除校车安全隐患,某市组织校车安全大检查.某校有A、B、C、D四辆校车,现分两天对其进行检测,每天检测两辆车,则A、B在同一天被检测的概率为()A.B.C.D.解析:选B基本事件是(AB,CD),(AC,BD),(AD,BC),(BC,AD),(BD,AC),(CD,AB),共有6个,其中A、B在同一天被检测的情况有(AB,CD),(CD,AB),共2个,故A、B在同一天被检测的概率为=.7.一个几何体的三视图如图所示,则这个几何体的体积为()A.B.C.D.解析:选A该几何体由底面半径为1的半圆锥与底面为边长等于2的正方形的四棱锥组成,且高都为,因此该几何体的体积为V=××+×(2×2)×=+=.8.如果执行如图所示的程序框图,输入正整数N(N≥2)和实数a1,a2…,,aN,输出A,B,则()A.A+B为a1,a2…,,aN的和B.(A+B)为a1,a2…,,aN的算术平均数C.A和B分别是a1,a2…,,aN中的最小数和最大数D.A和B分别是a1,a2…,,aN中的最大数和最小数解析:选D由图易知,该程序框图的功能是选择a1,a2…,,an中的最大数和最小数.9.(·郑州模拟)把70个面包分五份给5个人,使每个人所得成等差数列,且使较大的三份之和的是较小的两份之和,则最小的一份为()A.2B.8C.14D.20解析:选A由题意知,中间一份为14,设该等差数列的公差为d(d>0),则这五份分别是14-2d,14-d,14,14+d,14+2d.又(14+14+d+14+2d)=14-2d+14-d,解得d=6.故14-2d=2.10.给定命题p:函数y=sin和函数y=cos的图像关于原点对称;命题q:当x=kπ+(k∈Z)时,函数y=(sin2x+cos2x)取得极小值.下列说法正确的是()A.p∨q是假命题B.(綈p)∧q是假命题C.p∧q是真命题D.(綈p)∨q是真命题解析:选B命题p中y=cos=cos=cos=sin-与y=sin关于原点对称,故p为真命题;命题q中y=(sin2x+cos2x)=2sin取极小值时,2x+=2kπ-,则x=kπ-,k∈Z,故q为假命题,则(綈p)∧q为假命题.11.已知a,b,c∈(0∞,+),若3a-2b+c=0,则的()A.最大值是B.最小值是C.最大值是D.最小值是解析:选C因为b≤=,所以==,当且仅当3a=c时取等号.12.已知抛物线y2=8x的准线与双曲线-y2=1交于A,B两点,点F为抛物线的焦点,若△FAB为直角三角形,则双曲线的离心率是()A.B.C.2D.2解析:选B抛物线的准线方程为x=-2,设准线与x轴的交点为D(-2,0),由题意得∠AFB=90°,故|AB|=2|DF|=8,故点A的坐标为(-2,4).由点A在双曲线-y2=1上,可得-42=1,解得m=.故c2=m+1=,故双曲...