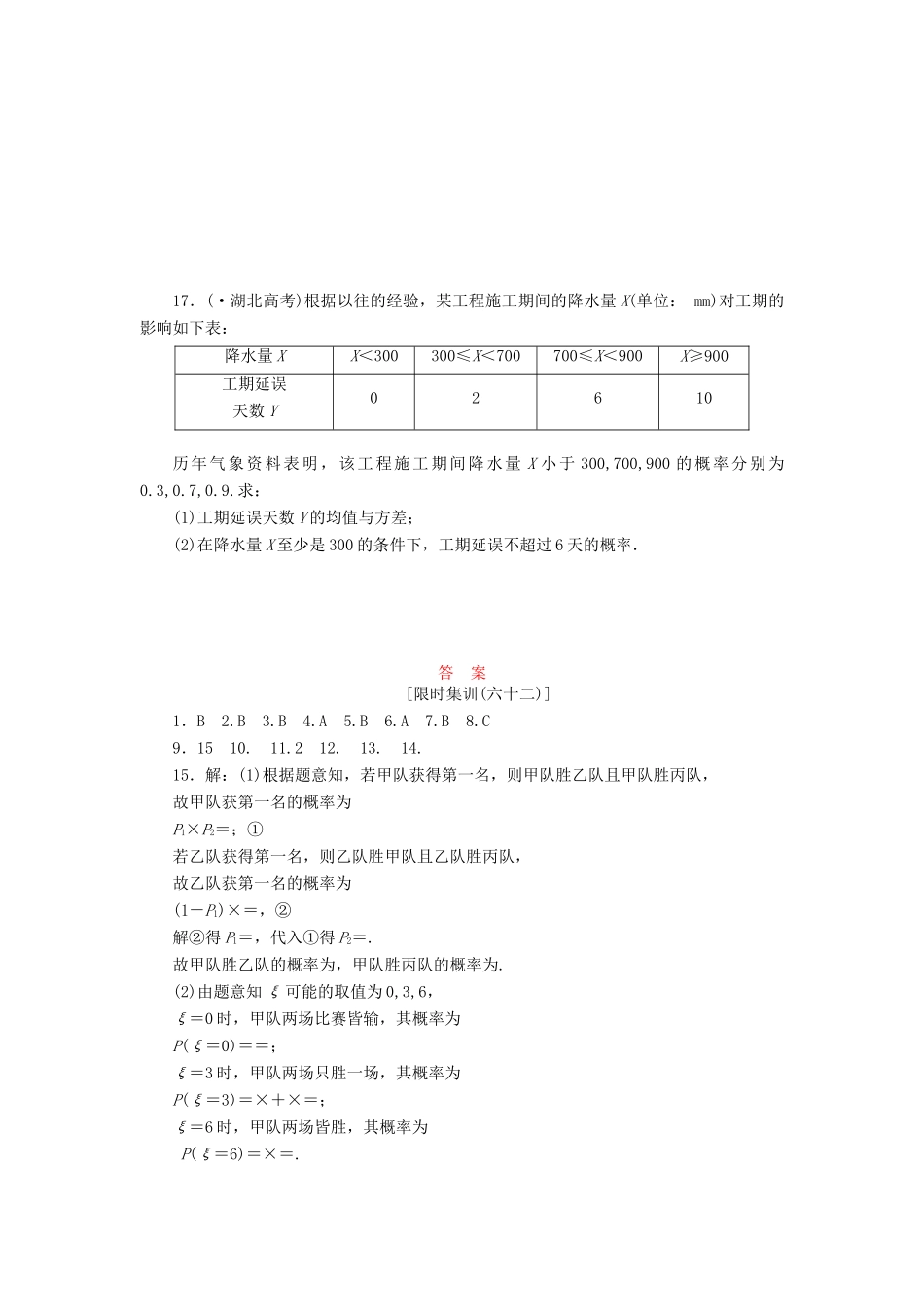
限时集训(六十二)离散型随机变量的均值与方差(限时:50分钟满分:106分)一、选择题(本大题共8个小题,每小题5分,共40分)1.设在各交通岗遇到红灯的事件是相互独立的,且概率都是0.4,则此人三次上班途中遇红灯的次数的期望为()A.0.4B.1.2C.0.43D.0.62.(·衡水模拟)若ξ~B(n,p)且E(ξ)=6,D(ξ)=3,则P(ξ=1)的值为()A.3·2-2B.3·2-10C.2-4D.2-83.(·东营模拟)若P为非负实数,随机变量ξ的分布列为ξ012P-PP则E(ξ)的最大值为()A.1B.C.D.24.有10件产品,其中3件是次品,从中任取2件,若X表示取到次品的个数,则E(X)等于()A.B.C.D.15.已知X的分布列为X-101P,且Y=aX+3,E(Y)=,则a为()A.1B.2C.3D.46.已知抛物线y=ax2+bx+c(a≠0)的对称轴在y轴的左侧,其中a,b,c∈{-3,-2,-1,0,1,2,3},在这些抛物线中,若随机变量ξ=|a-b|的取值,则ξ的数学期望E(ξ)=()A.B.C.D.7.一个篮球运动员投篮一次得3分的概率为a,得2分的概率为b,不得分的概率为c,a,b,c∈(0,1),且无其他得分情况,已知他投篮一次得分的数学期望为1,则ab的最大值为()A.B.C.D.8.体育课的排球发球项目考试的规则是:每位学生最多可发球3次,一旦发球成功,则停止发球,否则一直发到3次为止.设学生一次发球成功的概率为p(p≠0),发球次数为X,若X的数学期望E(X)>1.75,则p的取值范围是()A.B.C.D.二、填空题(本大题共6个小题,每小题4分,共24分)9.随机变量X的分布列为X124P0.40.30.3则E(5X+4)=________.10.同时抛两枚均匀的硬币10次,设两枚硬币出现不同面的次数为X,则D(X)=________.11.(·上海高考)马老师从课本上抄录一个随机变量ξ的概率分布列如下表:x123P(ξ=x)?!?请小牛同学计算ξ“”“”的数学期望.尽管!处完全无法看清,且两个?处字迹模糊,“”但能断定这两个?处的数值相同.据此,小牛给出了正确答案E(ξ)=________.12.(·沈阳模拟)设l为平面上过点(0,1)的直线,l的斜率等可能地取-2,-,-,0,,,2.用X表示坐标原点到l的距离,则随机变量X的数学期望E(X)=________.13.某大厦的一部电梯从底层出发后只能在第18,19,20层停靠,若该电梯在底层有5个乘客,且每位乘客在这三层的每一层下电梯的概率为,用ξ表示5位乘客在第20层下电梯的人数,则随机变量ξ的期望E(ξ)=________.14.现有三枚外观一致的硬币,其中两枚是均匀硬币另一枚是不均匀的硬币,这枚不均匀的硬币抛出后正面出现的概率为,现投掷这三枚硬币各1次,设ξ为得到的正面个数,则随机变量ξ的数学期望E(ξ)=________.三、解答题(本大题共3个小题,每小题14分,共42分)15.年男足世界杯将在巴西举行,为了争夺最后一个小组赛参赛名额,甲、乙、丙三支国家队要进行比赛,规则如下:任两支队伍进行比赛,共赛三场,每场比赛胜者得3分,负者得0分,没有平局,获得第一名的将夺得这个参赛名额.已知乙队胜丙队的概率为,甲队获得第一名的概率为,乙队获得第一名的概率为.(1)求甲队分别胜乙队和丙队的概率P1和P2;(2)设在该次比赛中,甲队得分为ξ,求ξ的分布列和数学期望.16.(·海淀模拟)某班将要举行篮球投篮比赛,比赛规则是:每位选手可以选择在A区投篮2次或选择在B区投篮3次.在A区每进一球得2分,不进球得0分;在B区每进一球得3分,不进球得0分,得分高的选手胜出.已知参赛选手甲在A区和B区每次投篮进球的概率分别为或.(1)如果选手甲以在A、B区投篮得分的期望较高者为选择投篮区的标准,问选手甲应该选择在哪个区投篮?(2)求选手甲在A区投篮得分高于在B区投篮得分的概率.17.(·湖北高考)根据以往的经验,某工程施工期间的降水量X(单位:mm)对工期的影响如下表:降水量XX<300300≤X<700700≤X<900X≥900工期延误天数Y02610历年气象资料表明,该工程施工期间降水量X小于300,700,900的概率分别为0.3,0.7,0.9.求:(1)工期延误天数Y的均值与方差;(2)在降水量X至少是300的条件下,工期延误不超过6天的概率.答案[限时集训(六十二)]1.B2.B3.B4.A5.B6.A7.B8.C9.1510.11.212.13.14.15.解:(1)根据题意知,若甲队获得第一名,则甲队胜乙队且甲队胜丙队,故甲队获第一...