含无限刚性杆弹簧支座结构的位移法VIP免费

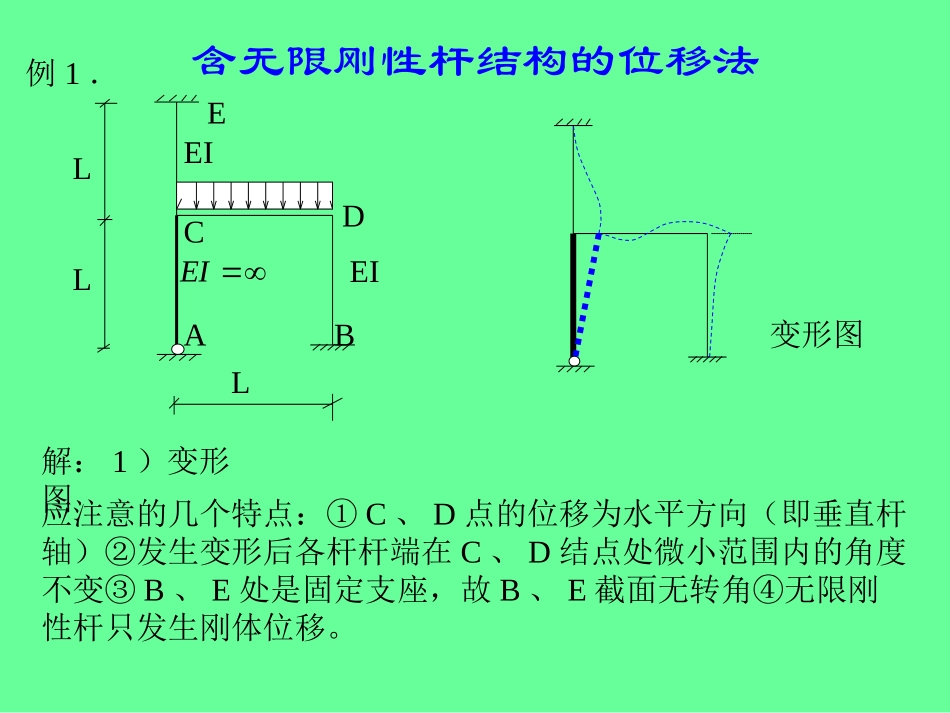
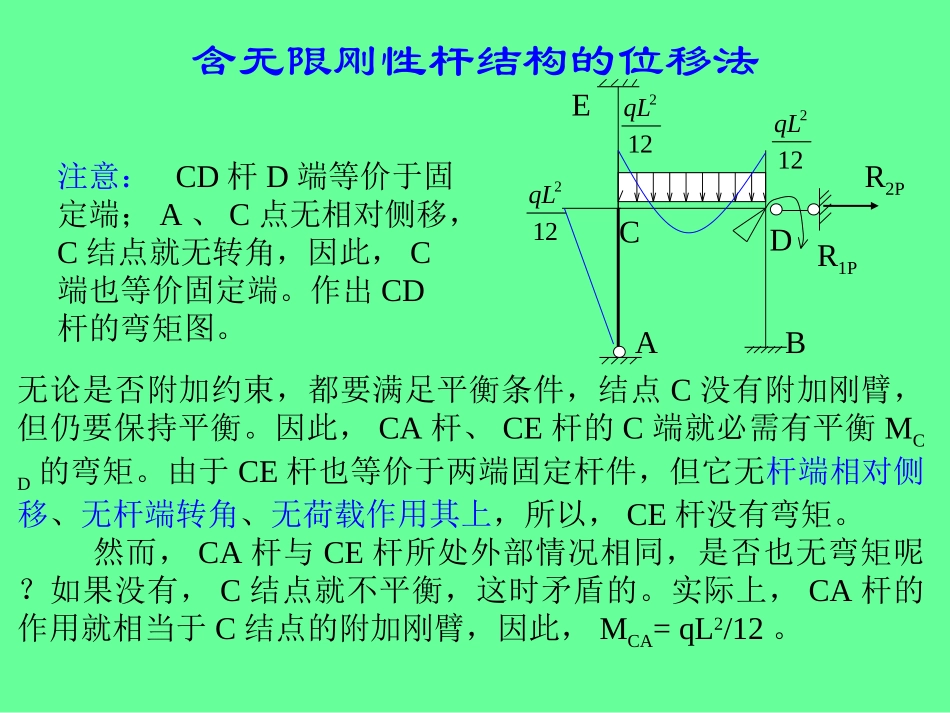
含无限刚性杆结构的位移法例1．ABCDELLLEIEIEI变形图解：1）变形图应注意的几个特点：①C、D点的位移为水平方向（即垂直杆轴）②发生变形后各杆杆端在C、D结点处微小范围内的角度不变③B、E处是固定支座，故B、E截面无转角④无限刚性杆只发生刚体位移。含无限刚性杆结构的位移法2）位移法变量：θD，ΔDH变形图DABC结点C虽然是刚结点，但与无限刚性杆CA连接，CA杆只发生侧移。CA杆的弦转角就是结点C的转角。即有关系LDHC3）附加约束，作MP图并求R1P，R2P122qL122qL122qLR1PR2P含无限刚性杆结构的位移法注意：CD杆D端等价于固定端；A、C点无相对侧移，C结点就无转角，因此，C端也等价固定端。作出CD杆的弯矩图。无论是否附加约束，都要满足平衡条件，结点C没有附加刚臂，但仍要保持平衡。因此，CA杆、CE杆的C端就必需有平衡MCD的弯矩。由于CE杆也等价于两端固定杆件，但它无杆端相对侧移、无杆端转角、无荷载作用其上，所以，CE杆没有弯矩。然而，CA杆与CE杆所处外部情况相同，是否也无弯矩呢？如果没有，C结点就不平衡，这时矛盾的。实际上，CA杆的作用就相当于C结点的附加刚臂，因此，MCA=qL2/12。122qL122qL122qLR1PR2PCDAEB含无限刚性杆结构的位移法122qL122qL122qLR1PR2PCDAEBR1PqL2/120D求R1P的研究对象VDBVCAVCER2P求R2P的研究对象R1P=qL2/12R2P=-qL/12含无限刚性杆结构的位移法r114i4i求r11的研究对象VCAVDBVCEr21=-4i/L求r21的研究对象ijrMM图，求图与作21)...4r114i4i2i2i2ir211M附加支杆后D结点转动的变形图r11D含无限刚性杆结构的位移法1r22附加刚臂后D结点水平移动的变形图2M6i/L8i/L10i/L4i/L2i/L6i/Lr22r12r12=-4i/Lr22=44i/L2含无限刚性杆结构的位移法1r22附加刚臂后D结点水平移动的变形图CDLiLiMCD414L1DCD*，所以，左端有转角端无转角，杆无相对侧移，LiLiLiMLiLiLiMECECCE826106141CE*端无转角，所以，端转角，，也有杆有相对侧移AELiMMCACA14,*可由结点平衡求得含无限刚性杆结构的位移法5）位移法方程002222111211PDHDPDHDRrrRrriqLD50452iqLDH100836）作M图DHDPMMMM2123qL2/50450qL2/50445qL2/504变形图含无限刚性杆结构的位移法例2．求作结构的弯矩图。L/2L/2LEIEI1EIPABCDP解：1）由于AB杆EI1=∞，故，位移法变量：ΔCH含无限刚性杆结构的位移法例2．2）附加支杆作MP图，并求R1PVBAR1PAD杆无杆端转角，无杆端相对侧移，无荷载，故，没有弯矩。BC杆无杆端转角，无杆端相对侧移，有荷载。AB为无限刚性杆，MBA与MBC平衡，MAB=0P3PL/16R1PABCDR1P=-3P/16含无限刚性杆结构的位移法例2．11)3rM图，求作3i/L3i/Lr11ABCDBC杆无杆端相对侧移，有B端的转角θB=1/LAD杆无杆端相对侧移，有A端的转角θA=1/LVBAr11r11=VBA=6i/L2含无限刚性杆结构的位移法例2．4）位移法方程，0111PCHRriPLCH3225）作M图CHPMMM3PL/323PL/32含无限刚性杆结构的位移法例3．求作结构的弯矩图。解：1）由于BD杆EA=∞，B、D点竖向位移相同，位移法变量：ΔDVABCDE变形图ABCDE20kN/m6m6m6mEA=∞含无限刚性杆结构的位移法例3．2）附加支杆作MP图，并求R1PR1P90ABCDEVBAVDAVDER1PkNVVVRDEDCBAP90751501附加支杆后，由于CD杆无穷刚性，所以D结点无转角。含无限刚性杆结构的位移法例3．11)3rM图，求作ABCDE变形图AB杆有杆端相对侧移Δ=1DE杆有杆端相对侧移Δ=-1，也有D端转角1/6LiLiLiMDE6131322221115663LiLiLiLiVVVrDEBADCr116i/L3i/L含无限刚性杆结构的位移法例3．4）位移法方程，0111PDVRriDV2165）作M图DVPMMM108126含无限刚性杆结构的位移法例4．求作结构的弯矩图。EI1=∞EI2EI2EI2m4m2m4mABCDE10kN/m解：1）位移法变量：ΔBV，θD2）附加约束，作MP图并求R1P，R2P含无限刚性杆结构的位移法例4．R1PR2P40/340/3ABCDEVBAVBCR1PR2PMDEMDCDR1P=-20/3R2P=40/3含无限刚性杆结构的位移法例4．ijrMM图，求图与作21)...3θ=1/2R11Δ=1R2PACDE先作出ΔBV=1时的变形图，观察各杆...