工程力学(下)第19-20章思考题VIP免费

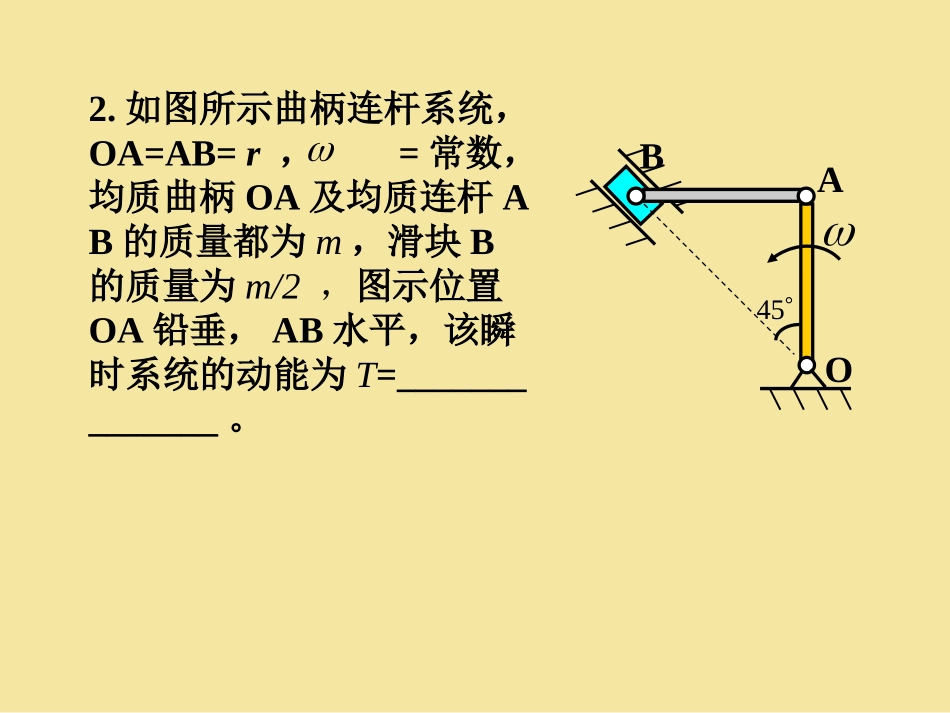
工程力学（工程力学（AA））北京理工大学理学院力学系韩斌((第第19-2019-20章思考题章思考题))（下册）（下册）§19-20§19-20动能定理动量原理思考题动能定理动量原理思考题1.图示均质杆AB，长为l，重量为P，A端以光滑铰链固定，杆AB可在铅垂平面内转动，C为杆的质心。当杆由水平位置无初速的摆到铅垂位置时，其动能为T，以下动能表达式中正确的为___________。（A）（B）（C）（D）gPlvgPTC821222gPllgPJTA63212122222gPllgPJTC2412212122222gPlJvgPTCC621212222（E）gPllgPvgPTC2473212122222ACBCv2.如图所示曲柄连杆系统，OA=AB=r，=常数，均质曲柄OA及均质连杆AB的质量都为m，滑块B的质量为m/2，图示位置OA铅垂，AB水平，该瞬时系统的动能为T=______________。45OABABAvBv(A)(C)(D)(B)221BBvm2)(21BABvvm)(2122BABvvm]sin)cos[(21222BBABvvvm3.三棱柱B放在三棱柱A上，沿着A的斜面运动，三棱柱A沿着光滑水平面向左运动，A的质量为mA，B的质量为mB，某瞬时A的速度为，B沿斜面的速度为，则此时三棱柱B的动能为T=____________。AvBv4.试判断下述说法是否正确：A.质点系的动量一定大于其中单个质点的动量。B.若质点系内各质点的动量皆为零，则质点系的动量必为零。C.若质点系内各质点的动量皆不为零，则质点系的动量必不为零。AC1BC2O5.右图中OA长l1，重P1，OB长l2，重P2，该瞬时系统的动量的大小为：222211lgPlgPp对吗？正确的应为什么？6.图示各均质刚体的质量均为m，求各刚体（或刚体系）在图示瞬时的动量和对固定点O的动量矩。2aaaOm（a）ROm（b）7.小球C和D质量均为m，焊接在不计质量、长2l的直杆CD两端，直杆中点焊接在铅垂轴z轴上，若杆CD绕铅垂z轴以匀角速度逆时针转动，则该质点系对转轴z轴的动量矩为_________________________________，动量矩的转向为________________。v30l3/lrmm（c）O7.小球C和D质量均为m，焊接在不计质量、长2l的直杆CD两端，直杆中点焊接在铅垂轴z轴上，若杆CD绕铅垂z轴以匀角速度逆时针转动，则该质点系对转轴z轴的动量矩为_________________________________，动量矩的转向为________________。CDzO题78.杆OA长为l，质量不计，均质圆盘半径为R，质量为m，圆心在A点，已知杆OA以角速度绕O轴顺时针转动，试求以下几种情形圆盘对定点O的动量矩：(A)圆盘固结于OA杆上；(B)圆盘铰接于杆的A点，绕A轴相对于杆以角速度转动；(C)圆盘铰接于杆的A点，绕A轴相对于杆以角速度转动；(D)圆盘以绝对角速度绕A轴转动；OA9.均质圆盘重P，半径为r，圆心为C，绕偏心轴O以角速度逆时针转动，偏心距OC=e，该圆盘对定轴O的动量矩为_______________________。(A)(B)(C)(D)2)(2ergP)2(222ergP)(222ergP222)2(4ergP10.图示机构，II轮质量为m,不计杆重，则系统对O点的动量矩)(2mlJJLIICIIOO，对吗？III题10rlOCCreO题911.图示均质杆AB，长为l，重量为P，A端以光滑铰链固定，杆AB可在铅垂平面内转动，C为杆的质心。当杆由水平位置无初速的摆到铅垂位置时，以下计算重力功的表达式中正确的为___________。ACB（A）（B）（C）（D）PllPW42222PllPW22cos20PldlPWPlW12.在下述哪些系统中机械能守恒？（A）其约束皆为理想约束的系统。（B）只有有势力作功的系统。（C）内力不作功的系统。（D）机械能不能转化为其他能量的系统。13.判断以下说法是否正确：动量守恒就意味着速度守恒，速度守恒就意味着动能守恒，故动量守恒时必有动能守恒。为什么？14.“摩擦力总是作负功”这个概念对吗？15.弹性系数为k的一弹簧下端吊一重物P后处于平衡状态，若弹簧的下端由该平衡位置向下移动时，弹性力作的功为，是否正确？若不对，请写出正确表达式。221kW16.判断以下4个过程中弹簧力作的功：（1）弹簧从原长拉长5cm，（2）弹簧从原长压缩5cm，（3）弹簧从拉长5cm后的位置再拉长5cm，（4）弹簧从拉长5cm后的位置再压缩5cm；这4个过程中弹簧力作的功是否相等...