刚体力学作业解答VIP免费

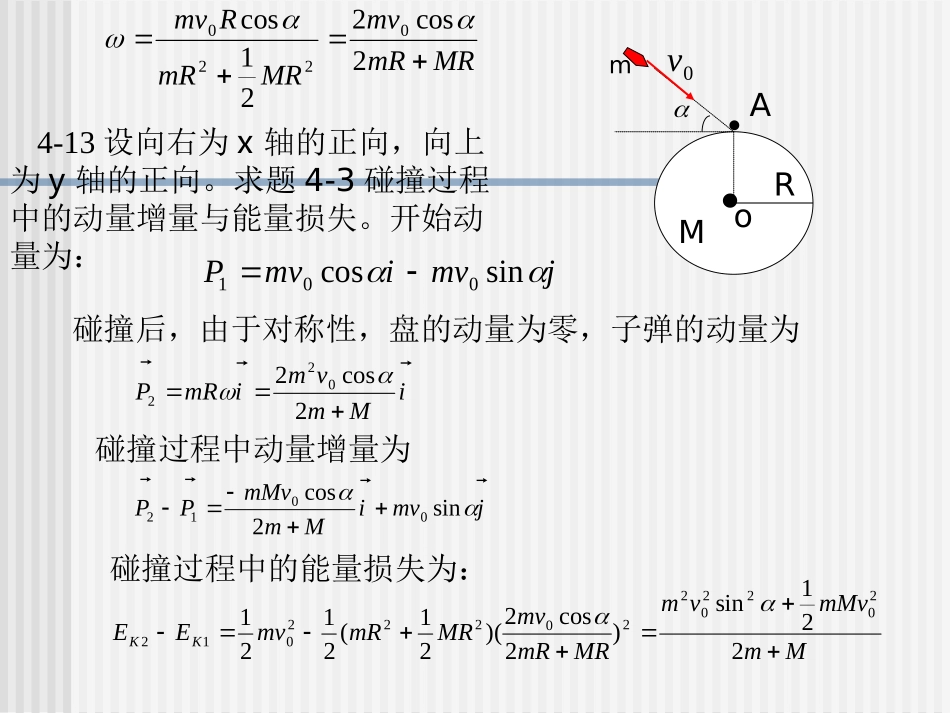
4-3RMm0vA子弹射入A的打击过程的守恒量(动能，动量，角动量）1完全非弹性碰撞，动能不守恒2轴对系统的作用力与冲力（m与M）有关，动量不守恒3角动量守恒4-12系统的角动量为多少？方向向内cos0RmvLo答案:(c)碰撞后系统的角速度:MRmRmvMRmRRmv2cos221cos0220jmvimvPsincos001iMmvmimRP2cos2022jmviMmmMvPPsin2cos0012MmmMvvmMRmRmvMRmRmvEEKK221sin)2cos2)(21(2121202202202220124-13设向右为x轴的正向，向上为y轴的正向。求题4-3碰撞过程中的动量增量与能量损失。开始动量为：碰撞后，由于对称性，盘的动量为零，子弹的动量为碰撞过程中动量增量为碰撞过程中的能量损失为：MRmRmvMRmRRmv2cos221cos0220RMm0vAo4-4已知银河系中有一天体是均匀球体，现在半径为R，绕对称轴自转的周期为T1，由于引力凝聚，它的体积不断收缩，预计一万年后它的半径缩小为r，则一万年后天体的自转周期T2与现在的自转周期T1的比值为，一万年后天体的转动动能E2与现在的转动动能E1的比值是。答案2212RrTT2212rREE4-5飞轮半径为0．10米，质量为2．0千克，边缘绕有绳子，现用恒力拉绳子的一端，使其由静止均匀地加速，经2.0秒转速达10转／秒。假定飞轮可看作实心圆柱体，求：(1)飞轮的角加速度及在这段时间内转过的转数；(2)拉力及拉力所作的功；(3)从拉动后t=10秒时飞轮的角速度及轮边缘上一点的速度、切向加速度和法向加速度。解：已知：飞轮质量M=2．0千克，半径0．10米，将飞轮看作实心圆柱体。其转动惯量是千克·米201.0212MRJ(1)已知：在t=2.0秒时，n=10转／秒，求角加速度和转数N弧度/秒2因此转过的角度为转数转tn且24.31102tnt20212t102N(2)由转动定律M=J=FR拉力拉力作功焦耳；(3)已知；t=10秒求按公式弧度／秒米／秒米／秒2米／秒2NRJF14.38.19JMAaavn,,,314100t4.3110Rv321014.3Ran14.3Ra习题4-6如图4-4（a）飞轮的质量m=60kg，半径R=0.5m，绕其水平中心轴O转动，转速为1000(r/min)。现利用一制动用的闸杆，在闸杆的一端加一竖直方向的制动力F，可使飞轮减速．已知闸杆的尺寸如图所示，闸瓦与飞轮之间的摩擦系数，飞轮的质量全部分布在外周上。4.0如要在5s内使飞轮转速减为零，需加多大的制动力F?题图4-4（a）m5.0Om75.0F解(1)先作闸杆和飞轮的受力分析如图4-4(b)（C）．图中N、是正压力，是摩擦力，和是转轴A对杆的作用力，杆受的重力忽略。mg是轮的重力，R是轮在O轴处所受支承力．杆处于静止状态，所以对A点的合力矩应为零，则有NrrFF、xFyF(a)0)(121lNllF闸瓦xFyxrFANyFF1l2l题图4-4(b)NmgOrFR题图4-4(c)FlllN121FlllN121NmgOrFR题图4-4(c)飞轮受到闸瓦的摩擦力为：(b)FlllNNFr121该摩擦力产生的转动力矩为RFMr对飞轮，按转动定律，其角加速度为121/2rFRllMdFtJJlJ24dJm11213142lmdFNllt)/(3333.131005.025.060)75.05.0(4.022srad由此可算出自施加制动闸开始到飞轮停止转动的时间为st07.7493333.132150这段时问内飞轮的角位移为)(253)49(3333.132107.721521220radtt可知在这段时间里，飞轮转了53转．(2)要求飞轮转速在t=2s内减少一半，可知20005.722sradtt用上面式(c)所示的关系，可求出所需的制动力为:NllmRlF177)(22114-7一轻绳绕于半径r=0．2m的飞轮边缘，现以恒力F=98N拉绳的一端，使飞轮由静止开始加速转动，如图4-5.(a)．已知飞轮的转动惯量J=0．5kg·m。，飞轮与轴承之间的摩擦不计．求。(1)飞轮的角加速度；(2)绳子拉下5m时，飞轮的角速度和飞轮获得的动能；(3)这动能和拉力F所作的功是否相等?为什么?(4)如以重量P=98N的物体m挂在绳端，如图4-5(b)，飞轮将如何运动?试再计算飞轮的角加速度和绳子拉...