方程的跟与函数的零点VIP免费

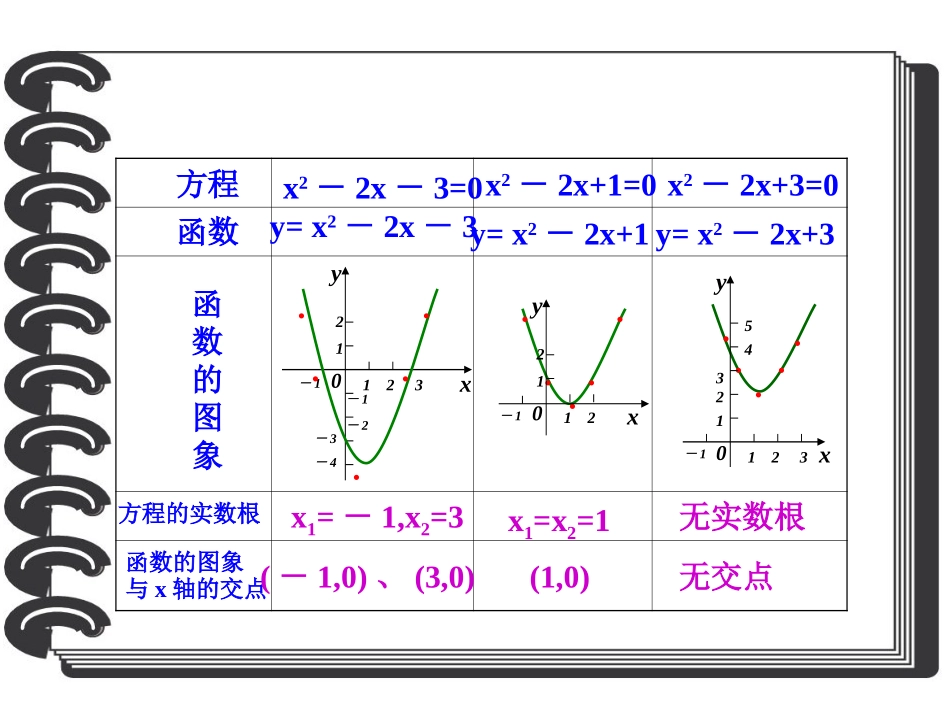
3.1.1方程的根与函数的零点方程x2－2x+1=0x2－2x+3=0y=x2－2x－3y=x2－2x+1函数函数的图象方程的实数根x1=－1,x2=3x1=x2=1无实数根函数的图象与x轴的交点(－1,0)、(3,0)(1,0)无交点x2－2x－3=0xy0－132112－1－2－3－4..........xy0－132112543.....yx0－12112y=x2－2x+3从上面的表格，你能发现方程的根与函数图象与X轴的交点具有什么样的关系吗？方程的根就是函数图象与X轴交点的横坐标。探究活动对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点。函数零点的定义：函数零点的定义：注意：零点指的是一个实数；方程f(x)=0有实数根函数y=f(x)的图象与x轴有交点函数y=f(x)有零点等价关系等价关系::思考：零点是点吗？求零点的方法•(1)解方程：令f(x)=0,解x。•（2）图像法：作y=f(x)的图像，看图像与x轴的交点的横坐标。练习求下列函数的零点：（1）（2）（3）xxfln)(1)(xexfxxxf4)(3解:（1）1；（2）0；（3）—2、0、2如图所示，用几条连续不断的函数图象连接A、B两点。动一动手﹒﹒ABL﹒﹒ABLOXyOyXOyXababab﹒﹒ABL﹒﹒ABL思考：通过对图象的观察，分析函数在区间端点上的函数值的符号情况，与函数零点是否存在着一定的关系呢？0)()(bfafabxxf1)(0)()(bfaf有，但在区间(a，b)内无零点。0)()(bfaf是否只要满足，就一定存在零点呢？函数零点存在性定理如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线，并且有f(a)·f(b)<0，那么，函数y=f(x)在区间(a,b)内有零点，即存在c(a,b)∈，使得f(c)=0，这个c也就是方程f(x)=0的根。（1）若函数y=f(x)在区间[a,b]上连续，且有f(a)·f(b)>0,则y=f(x)在区间(a,b)内是否有零点？想一想OyX2)(xxfab（2）若函数y=f(x)在区间[a,b]上连续，且有f(a)·f(b)<0,则y=f(x)在区间(a,b)内会只有一个零点吗？OXyab﹒﹒ABL﹒﹒ABLOyXab（3）若函数y=f(x)在区间[a,b]上连续，且在区间(a,b)内有零点时，一定有f(a)·f(b)<0吗？OyX2)(xxfab注意：（1）只有同时满足上述两个条件，才能说明函数y=f(x)在区间(a,b)内存在零点。（2）定理不可逆。例1、判断函数是否存在零点？53)(3xxxf例2、求函数的零点的个数？62ln)(xxxf想一想函数y=f(x)在什么条件下，在区间(a,b)内只有一个零点？结论函数y=f(x)在区间(a,b)内单调时，函数在这个区间内有且只有一个零点。2(2)2(2)解：解：作出函数的图象如下：........因为f(3)＝－3<0,f(4)≈2.545>0,所以f(x)=2x·ln(x－2)－3在区间(3,4)上有零点。又因为f(x)=2x·ln(x－2)－3是(2，＋∞）上的增函数，所以在区间(3,4)上有且只有一个零点。xy0－1321125-3-242(2)f(x)=2x·ln(x－2)－32(3)2(3)解：解：作出函数的图象如下：........因为f(0)≈－3.63<0,f(1)＝1>0,所以f(x)=ex－1+4x－4在区间(0,1)上有零点。又因为f(x)=ex－1+4x－4是(－∞，＋∞）上的增函数，所以在区间(0,1)上有且只有一个零点。2(3)f(x)=ex－1+4x－4xy0－132112－1－2－3－4－242(4)2(4)解：解：作出函数的图象如下：x0－80－1－55y24012043－60－40－20－4－3－2因为f(－4)＝－4<0,f(－3)＝15>0,f(－2)＝－2<0,f(2)＝－70<0,f(3)＝3>0,所以f(x)=3(x+2)(x－3)(x+4)+x在区间(－4,－3)、(－3，－2,)、(2,3)上各有一个零点。2(4)f(x)=3(x+2)(x－3)(x+4)+x......................小结函数零点的定义求零点的方法求零点的方法函数的零点存在的判定定理布置作业：P92习题3.1第2题三维设计课时训练十八