第三讲 第二章单跨梁的弯曲理论VIP免费

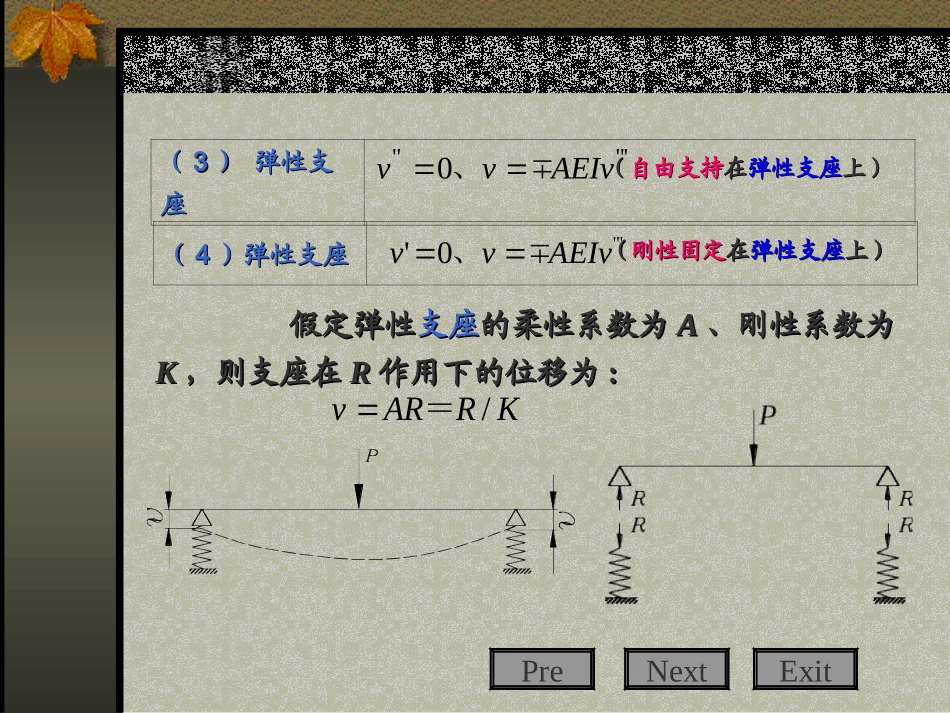
第二章单跨梁的弯曲理论第二章单跨梁的弯曲理论§2-1梁的弯曲微分方程式及积分§2-2梁的支座及边界条件§2-3梁的弯曲要素表及应力计算§2-4剪切对梁弯曲变形的影响ExitNextPre（（11）自由支）自由支持持)(00''"EIvMvv、（（22）刚性固）刚性固定定）（、000'vv不同的支座对梁有不同的约束，因而就给出不同的边界条件，不同的支座对梁有不同的约束，因而就给出不同的边界条件，梁端的边界条件就是梁端弯曲要素的特定值或梁端的边界条件就是梁端弯曲要素的特定值或弯曲要素之间的特定关系，它们取决于梁端的支座情弯曲要素之间的特定关系，它们取决于梁端的支座情况。况。不允许梁端发生挠度，而对梁不允许梁端发生挠度，而对梁的转动无限制的转动无限制梁在刚性固定端处挠度与转角均为零而梁在刚性固定端处挠度与转角均为零而弯矩、剪力不等于零弯矩、剪力不等于零§2-2§2-2梁的支座及边界条件梁的支座及边界条件ExitNextPre（（33）弹性支）弹性支座座（（自由支持自由支持在在弹性支座弹性支座上）上）'""0AEIvvv、假定弹性假定弹性支座支座的柔性系数为的柔性系数为AA、、刚性系数为刚性系数为KK，，则支座在则支座在RR作用下的位移为作用下的位移为::KRARv/＝（（44）弹性支座）弹性支座（（刚性固定刚性固定在在弹性支座弹性支座上）上）"'0'AEIvvv、ExitNextPre（（44）弹性固定端）弹性固定端（弹性固定弹性固定在刚性支座上）"'0EIvvv、假定弹性固定端的柔性系数为假定弹性固定端的柔性系数为aa、、刚性系数刚性系数为为KK，，则固定端在则固定端在MM作用下的转角为作用下的转角为::KMM/＝（（55）弹性支座）弹性支座（弹性固定弹性固定在弹性支座弹性支座上）"'"'"':"':EIvvAEIvvEIvvAEIvv、右端、左端例例11求两端自由支持在刚性支座上，受均布荷重作用的梁的挠曲求两端自由支持在刚性支座上，受均布荷重作用的梁的挠曲线线解解均布荷重均布荷重qq，，沿梁长分布，则沿梁长分布，则2340000000026xxxxMxNxqxdxEIEIEI式中的积分，当式中的积分，当qq==常数时可得：常数时可得：44000024xxxxqqxdxEIEI考虑到梁左端自由支持在刚性支座上，考虑到梁左端自由支持在刚性支座上，0000,/2MNql又所以所以3401224qlxqxxEIEI00xl式中式中要由梁右支座的边界条件要由梁右支座的边界条件求出，将求出，将代入上式，得：代入上式，得：44001224qlqllEIEI3n24qlEI故故挠曲线方程式为：挠曲线方程式为：33443434224122424qlxqlxqxqlxxxEIEIEIEIlll应用举例ExitNextPre例例22求下图中所示受集中力作用的单跨梁的挠曲线方程式。梁求下图中所示受集中力作用的单跨梁的挠曲线方程式。梁的左端为弹性固定端，柔性系数为；梁的左端为弹性固定端，柔性系数为；梁的右端为弹性支座，柔性系数为。的右端为弹性支座，柔性系数为。)3/(EIl＝)48/(3EIlA＝ExitNextPre解：（1）列通式（2）列边界条件(a)EIlxPEIxNEIxMxvvl6)2/(6232/302000EIlxPEIxNEIMvl)2/(2/00EIPEINvl2/00000,0Mvx、时当EIlxPEIxNEIxMEIlxMvl6)2/(62332/30200ExitNextPre(b)vAEIvvlxll、时当0,''0200＝EIPlEIlNEIM)(486)2/(623033302020PNEIlEIlPEIlNEIlMEIlM(4)列求解结果32/33223)2(33202273376llxlxlxlxEIPlvlPNPlM332066700＝＝