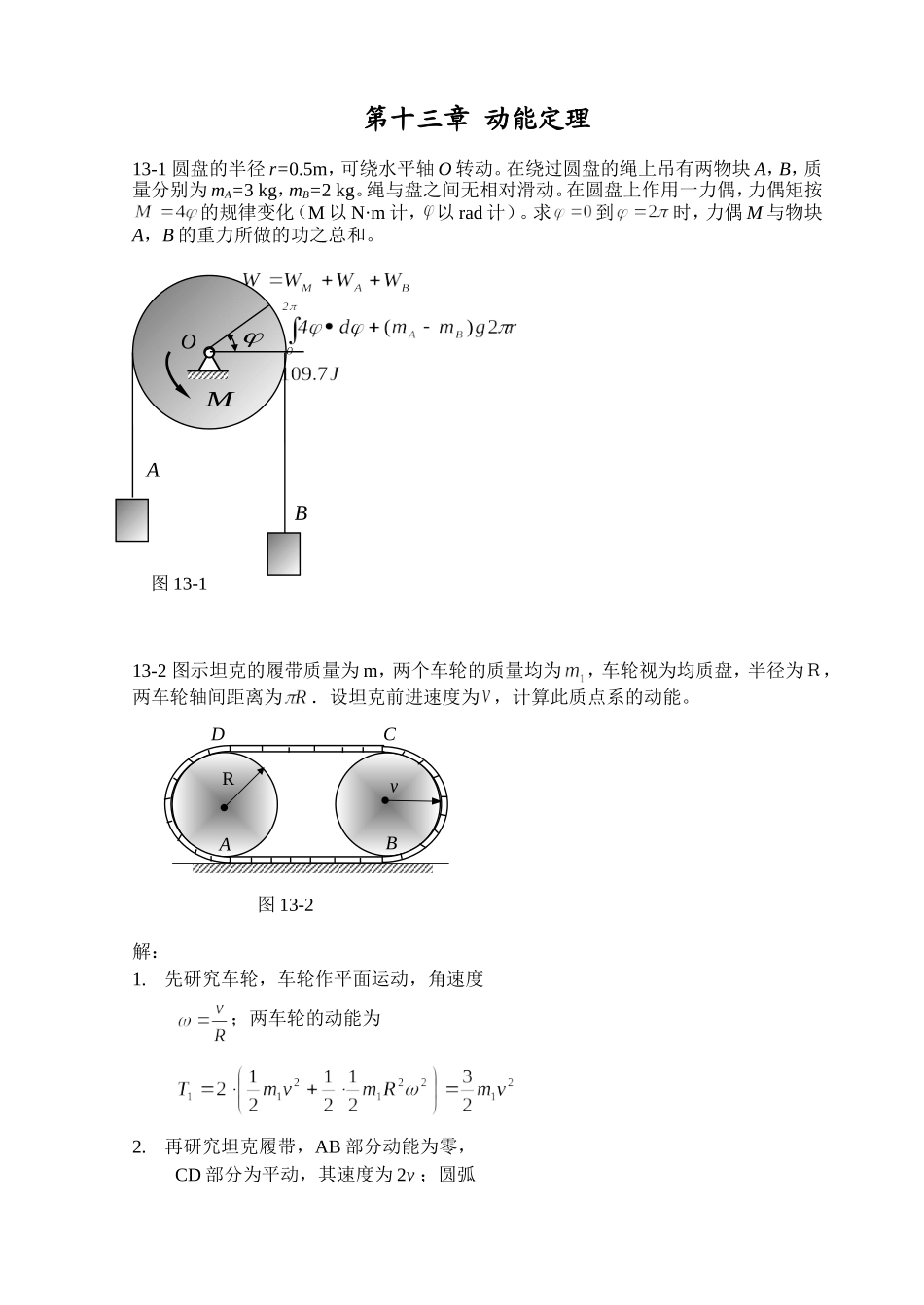
第十三章动能定理13-1圆盘的半径r=0.5m,可绕水平轴O转动。在绕过圆盘的绳上吊有两物块A,B,质量分别为mA=3kg,mB=2kg。绳与盘之间无相对滑动。在圆盘上作用一力偶,力偶矩按的规律变化(M以N·m计,以rad计)。求到时,力偶M与物块A,B的重力所做的功之总和。13-2图示坦克的履带质量为m,两个车轮的质量均为,车轮视为均质盘,半径为R,两车轮轴间距离为.设坦克前进速度为,计算此质点系的动能。解:1.先研究车轮,车轮作平面运动,角速度;两车轮的动能为2.再研究坦克履带,AB部分动能为零,CD部分为平动,其速度为2v;圆弧图13-2DCRABvOABM图13-1AD与BC部分和起来可视为一平面运动圆环,环心速度为v,角速度为,则履带的动能为3.此质点系的动能为13-3均质连杆AB质量为4kg,长l=600mm。均质圆盘质量为6kg,半径r=100mm。弹簧刚度为k=2N/mm,不计套筒A及弹簧的质量。如连杆在图示位置被无初速释放后,A端沿光滑杆滑下,圆盘做纯滚动。求:(1)当AB达水平位置而接触弹簧时,圆盘与连杆的角速度;(2)弹簧的最大压缩量δ。13-4质量为m,沿倾角为的斜面向下只滚不滑,如图所示。滚子借助于跨过滑轮B的绳提升质量为的物体C,同时滑轮B绕O轴转动。滚子A与滑轮B的质量相等,半径相等,且都为均质圆盘。求滚子重心的加速度AB30图13-3解:设滚子质心下滑距离S时,质心的速度为以整体为研究对象,设滚子半径为R,该系统的动能为将代入,得由动能定理得,将上式两边对时间求导得13-5均质圆盘与杆OA焊在一起,可绕水平轴O转动,如图所示。已知杆OA长l,质量为m1;圆盘半径为R,质量为m2。摩擦不计,初始时杆OA水平,杆和圆盘静止。求杆与水平线成θ角的瞬时,杆的角速度和角加速度。AOA图13-5图13-4AOBC13-6三个均质轮、、,具有相同的质量和相同的半径,绳重不计,系统从静止释放。设轮作纯滚动,绳的倾斜段与斜面平行。试求在重力作用下,质量亦为的物体下落时的速度和加速度。ABDC图13-6