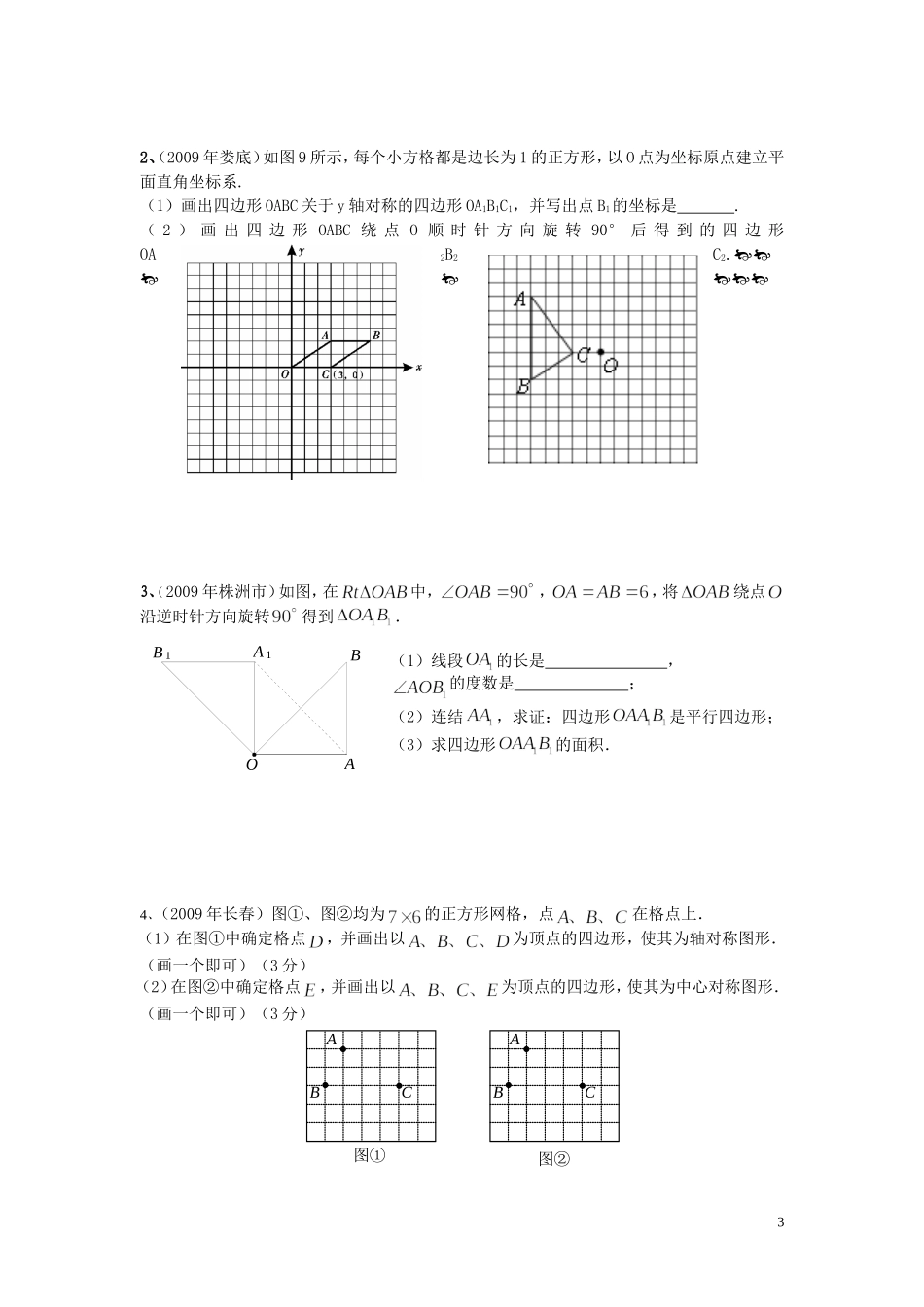
旋转单元总结与复习一、课前十分钟练习1、解下列方程:(1)(2)(3)3x2–4x–1=0()(4)4x2–8x+1=0(用配方法)(5)(6)2、应用题Ⅰ、如图,某海军基地位于A处,在其正南方向200海里处有一重要目标B,在B的正东方向200海里处有一重要目标C,小岛D位于AC的中点,岛上有一补给码头:小岛F位于BC上且恰好处于小岛D的正南方向,一艘军舰从A出发,经B到C匀速巡航,一般补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰.(1)小岛D和小岛F相距多少海里?(2)已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行了多少海里?(结果精确到0.1海里)BACEDwww.czsx.com.cnF1Ⅱ、某商店经销一种销售成本为每千克40元的水产品,据市场分析,若每千克50元销售,一个月能售出500kg,销售单价每涨1元,月销售量就减少10kg,针对这种水产品情况,请解答以下问题:(1)当销售单价定为每千克55元时,计算销售量和月销售利润.(2)设销售单价为每千克x元,月销售利润为y元,求y与x的关系式.(3)商品想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应为多少?二、基本概念1、旋转:把一个图像绕着某一点O转动一个角度的图像变换叫做旋转,点O叫做旋转中心,转动的角叫做旋转角。(旋转三要素是什么?)想一想:什么叫做对应点?2、中心对称:把一个图形绕着某一个点旋转,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心,这两个图形中的对应点叫做关于中心的对称点。3、中心对称图形:把一个图形绕着某一个点旋转,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心。4、关于原点对称的点的坐标:两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点的对称点是_______。注意:1、对应点到旋转中心的距离相等。对应点与旋转中心所连线段的夹角等于旋转角。旋转前后的图形全等。2、关于中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分.关于中心对称的两个图形是全等图形.三、典型例题:1、(2009年绵阳)如图是由若干个边长为1的小正方形组成的网格,请在图中作出将“蘑菇”ABCDE绕A点逆时针旋转90再向右平移2个单位的图形(其中C、D为所在小正方形边的中点)。2ABECDB1AOBA12、(2009年娄底)如图9所示,每个小方格都是边长为1的正方形,以O点为坐标原点建立平面直角坐标系.(1)画出四边形OABC关于y轴对称的四边形OA1B1C1,并写出点B1的坐标是.(2)画出四边形OABC绕点O顺时针方向旋转90°后得到的四边形OA2B2C2.3、(2009年株洲市)如图,在中,,,将绕点沿逆时针方向旋转得到.(1)线段的长是,的度数是;(2)连结,求证:四边形是平行四边形;(3)求四边形的面积.4、(2009年长春)图①、图②均为的正方形网格,点在格点上.(1)在图①中确定格点,并画出以为顶点的四边形,使其为轴对称图形.(画一个即可)(3分)(2)在图②中确定格点,并画出以为顶点的四边形,使其为中心对称图形.(画一个即可)(3分)3ABC图①ABC图②5、(2009年河南)如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2.点0是AC的中点,过点0的直线l从与AC重合的位置开始,绕点0作逆时针旋转,交AB边于点D.过点C作CE∥AB交直线l于点E,设直线l的旋转角为α.(1)①当α=________度时,四边形EDBC是等腰梯形,此时AD的长为_________;②当α=________度时,四边形EDBC是直角梯形,此时AD的长为_________;(2)当α=90°时,判断四边形EDBC是否为菱形,并说明理由.四、观察探索对于四边形ABCD1、旋转中心不变,改变旋转角画出以下图所示的四边形ABCD以O点为中心,旋转角分别为30°、60°的旋转图形.2、旋转角不变,改变旋转中心画出以下图,四边形ABCD分别为O、O为中心,旋转角都为30°的旋转图形.因此,从以上的画图中,我们可以得到旋转中心不变,改变()与旋转角不变,改变旋4转()会产生()的效果,所以,我们可以经过旋转设计出美丽的图案.5