函数的奇偶性与周期性VIP免费

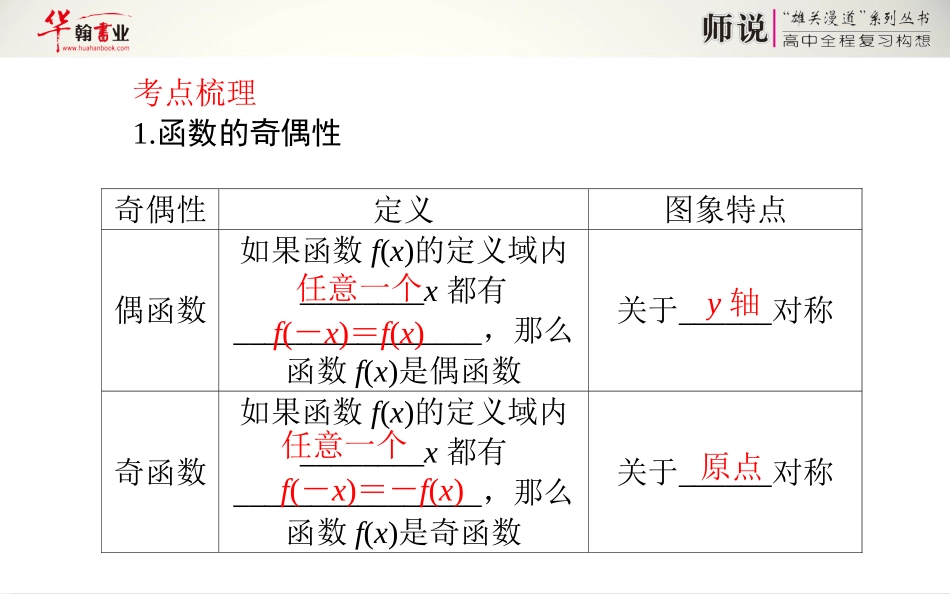
1．5函数的奇偶性与周期性考点梳理1.函数的奇偶性奇偶性定义图象特点偶函数如果函数f(x)的定义域内________x都有________________，那么函数f(x)是偶函数关于______对称奇函数如果函数f(x)的定义域内________x都有________________，那么函数f(x)是奇函数关于______对称任意一个f(－x)＝f(x)y轴任意一个f(－x)＝－f(x)原点2.奇偶函数的性质(1)奇函数在关于原点对称的区间上的单调性________，偶函数在关于原点对称的区间上的单调性________(填“相同”、“相反”)．(2)在公共定义域内①两个奇函数的和函数是________，两个奇函数的积函数是________.②两个偶函数的和函数、积函数是________.③一个奇函数与一个偶函数的积函数是________.(3)若f(x)是奇函数且在x＝0处有定义，则f(0)＝________.相同相反奇函数偶函数偶函数奇函数03．函数的周期性(1)周期函数：对于函数y＝f(x)，如果存在一个非零常数T，使得当x取定义域内的任何值时，都有f(x＋T)＝_______，那么就称函数y＝f(x)为周期函数，称T为这个函数的周期．(2)最小正周期：如果在周期函数f(x)的所有周期中_________________的正数，那么这个_________就叫做f(x)的最小正周期．(3)常见结论：①若f(x＋a)＝－f(x)，则T＝2a；②若f(x＋a)＝1fx，则T＝2a；③若f(x＋a)＝－1fx，则T＝2a.(4)若f(x)为奇函数且周期为T，则fT2＝0.f(x)存在一个最小最小正数考点自测1.已知f(x)＝ax2＋bx是定义在[a－1,2a]上的偶函数，那么a＋b的值是()A．－13B.13C.12D．－12解析：由题意得a－1＝－2a且b＝0，故a＝13，a＋b＝13，选B.答案：B2．已知y＝f(x)是定义在R上的奇函数，则下列函数中是奇函数的是()①y＝f(|x|)；②y＝f(－x)；③y＝xf(x)；④y＝f(x)＋x.A．①③B．②③C．①④D．②④解析：由奇函数的定义验证可知②④正确，选D.答案：D3．若函数f(x)＝x2x＋1x－a为奇函数，则a＝()A.12B.23C.34D．1解析：由题意，得f(－1)＝－f(1)，即－1－1×－1－a＝－131－a，解得a＝12，选A.答案：A4．已知f(x)在R上是奇函数，且满足f(x＋4)＝f(x)，当x∈(0,2)时，f(x)＝2x2，则f(7)＝()A．－2B．2C．－98D．98解析：由f(x＋4)＝f(x)，得f(7)＝f(3)＝f(－1)，又f(x)为奇函数，∴f(－1)＝－f(1)，f(1)＝2×12＝2，∴f(7)＝－2.故选A.答案：A5．若函数f(x)＝x2－|x＋a|为偶函数，则实数a＝__________.解析：由题意，得f(－x)＝f(x)∀x∈R恒成立，即x2－|－x＋a|＝x2－|x＋a|∀x∈R恒成立．故|x＋a|＝|x－a|∀x∈R恒成立．所以(x＋a)2＝(x－a)2，即4ax＝0对x∈R恒成立．从而a＝0.答案：0疑点清源1.函数奇偶性的判断判断函数的奇偶性主要根据定义：一般地，如果对于函数f(x)的定义域内任意一个x，都有f(－x)＝f(x)(或f(－x)＝－f(x))，那么函数f(x)就叫做偶函数(或奇函数)．其中包含两个必备条件：①定义域关于原点对称，这是函数具有奇偶性的必要不充分条件，所以首先考虑定义域有利于准确简捷地解决问题；②判断f(x)与f(－x)是否具有等量关系．在判断奇偶性的运算中，可以转化为判断奇偶性的等价关系式(f(x)＋f(－x)＝0(奇函数)或f(x)－f(－x)＝0(偶函数))是否成立．2．函数奇偶性的性质(1)奇函数在关于原点对称的区间上若有单调性，则其单调性完全相同；偶函数在关于原点对称的区间上若有单调性，则其单调性恰恰相反．(2)若f(x)为偶函数，则f(－x)＝f(x)＝f(|x|)．(3)若奇函数f(x)定义域中含有0，则必有f(0)＝0.f(0)＝0是f(x)为奇函数的既不充分也不必要条件．(4)定义在关于原点对称区间上的任意一个函数，都可表示成“一个奇函数与一个偶函数的和(或差)”．(5)复合函数的奇偶性特点是：“内偶则偶，内奇同外”．(6)既奇又偶的函数有无穷多个(如f(x)＝0，定义域是关于原点对称的任意一个数集)．3．关于周期函数的常用结论(1)若对于函数f(x)定义域内的任意一个x都有：①f(x＋a)＝－f(x)，则函数f(x)必为周期函数，2|a|是它的一个周期；②f(x＋a)＝1fx，则函数f(x)必为周期函数，2|a|是它的一个周期；③f(x＋a)＝－1fx，则函数f(x)必为周期函数，2|a|是它的一个周期；(2)如果T是函数y＝f(x)的周期，则①kT(k...