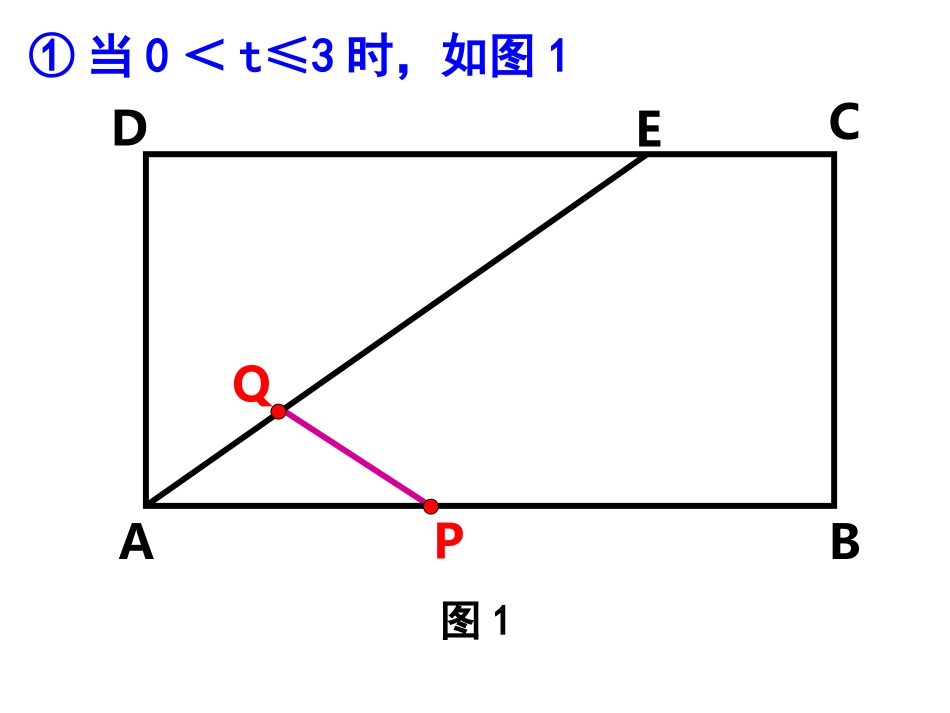
动态型问题除了固定不变的几何条件外,还有一个运动变化的特点,即点动、线动或几何图形动等,其中点动是基础,线动和图形动可转换为点动。在解这类问题时,要充分发挥空间想象的能力,不要被“动”所迷惑,而是要在“动”中求“静”,化“动”为“静”,抓住它运动中的某一瞬间,寻找确定的关系式,就能找到解决问题的途径。动点问题1.如图,矩形ABCD中,AB=6cm,AD=3cm,点E在边DC上,且DE=4cm.动点P从点A开始沿着ABCE⇒⇒⇒的路线以2cm/s的速度移动,动点Q从点A开始沿着AE以1cm/s的速度移动,当点Q移动到点E时,点P停止移动.类型1:点动若点P、Q同时从点A同时出发,设点Q移动时间为t(s),P、Q两点运动路线与线段PQ围成的图形面积为S(cm2),求S与t的函数关系式.①当0<t≤3时,如图1图1CEDBAQP②当3<t≤9/2时,如图2图2CEDBAQP②当9/2<t≤5时,如图3图3CEDBAQP变式训练:如图:已知□ABCD中,AB=7,BC=4,∠A=30°(1)点P从点A沿AB边向点B运动,速度为1cm/s。若设运动时间为t(s),连接PC,当t为何值时,△PBC为等腰三角形?(2)若点P从点A沿射线AB运动,速度仍是1cm/s。当t为何值时,△PBC为等腰三角形?3)当t>7时,是否存在某一时刻t,使得线段DP将线段BC三等分?DCBA2.如图,在Rt△ABC中,∠C=90°,AC=BC=4cm,点D为AC边上一点,且AD=3cm,动点E从点A出发,以1cm/s的速度沿线段AB向终点B运动,运动时间为xs.作∠DEF=45°,与边BC相交于点F.设BF长为ycm.(1)当x=s时,DE⊥AB;(2)求在点E运动过程中,y与x之间的函数关系式及点F运动路线的长;(3)当△BEF为等腰三角形时,求x的值.3.如图,已知直线l1的解析式为y=3x+6,直线l1与x轴,y轴分别相交于A,B两点,直线l2经过B,C两点,点C的坐标为(8,0),又已知点P在x轴上从点A向点C移动,点Q在直线l2从点C向点B移动.点P,Q同时出发,且移动的速度都为每秒1个单位长度,设移动时间为t秒(1<t<10).(1)求直线l2的解析式;(2)设△PCQ的面积为S,求出S关于t的函数关系式;(3)试探究:当t为何值时,△PCQ为等腰三角形?4.如图,在等腰梯形ABCD中,AB∥CD,AB=8cm,AD=6cm,∠A=60°.(1)求梯形ABCD的面积;(2)点P从点A出发,以2cm/s的速度沿AB向终点B运动;点Q从点C出发,以1cm/s的速度沿CD向终点D运动(P,Q两点中,有一点运动到了终点,所有运动即终止),设P、Q同时出发并运动了t秒.153t=5/3不存在①当PQ将梯形ABCD分成两个直角梯形时,求t的值;②试问是否存在这样的t,使四边形PBCQ的面积是梯形ABCD面积的一半?若存在,求出这样的t的值;若不存在,说明理由.5.如图在梯形ABCD中,DC∥AB,∠A=90°,AD=6厘米,DC=4厘米,BC的坡度i=3:4,动点P从A出发以2厘米/秒的速度沿AB方向向点B运动,动点Q从点B出发以3厘米/秒的速度沿BCD⇒⇒方向向点D运动,两个动点同时出发,当其中一个动点到达终点时,另一个动点也随之停止.设动点运动的时间为t秒.①求边BC的长;②当t为何值时,PC与BQ相互平分;③连接PQ,设△PBQ的面积为y,探求y与t的函数关系式,求t为何值时,y有最大值?最大值是多少?6.如图1,在等腰梯形ABCD中,AB∥DC,AD=BC=4cm,AB=12cm,CD=8cm点P从A开始沿AB边向B以3cm/s的速度移动,点Q从C开始沿CD边向D以1cm/s的速度移动,如果点P、Q分别从A、C同时出发,当其中一点到达终点时,另一点也随之停止运动.设运动时间为t(s).(1)t为何值时,四边形APQD是平行四边形?(2)如图2,如果⊙P和⊙Q的半径都是2cm,那么,t为何值时,⊙P和⊙Q外切?(1) DQ∥AP,∴当AP=DQ时,四边形APQD是平行四边形.此时,3t=8-t.解得t=2(s).即当t为2s时,四边形APQD是平行四边形.(2) ⊙P和⊙Q的半径都是2cm,∴当PQ=4cm时,⊙P和⊙Q外切.而当PQ=4cm时,如果PQ∥AD,那么四边形APQD是平行四边形.①当四边形APQD是平行四边形时,由(1)得t=2.②当四边形APQD是等腰梯形时,∠A=∠APQ. 在等腰梯形ABCD中,∠A=∠B,∴∠APQ=∠B.∴PQ∥BC.∴四边形PBCQ平行四边形.此时,CQ=PB.∴t=12-3t.解得t=3(s).综上,当t为2s或3s时,⊙P和⊙Q相切.7.已知:如图,四边形ABCD是等腰梯形,其中AD∥B...