初二下勾股定理课件(3)VIP免费

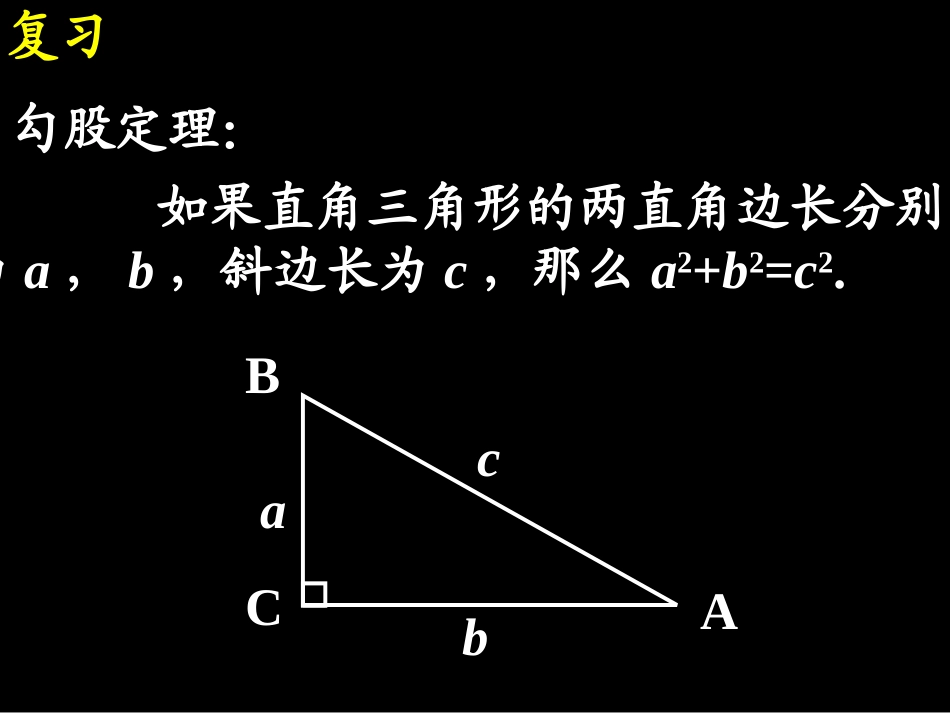
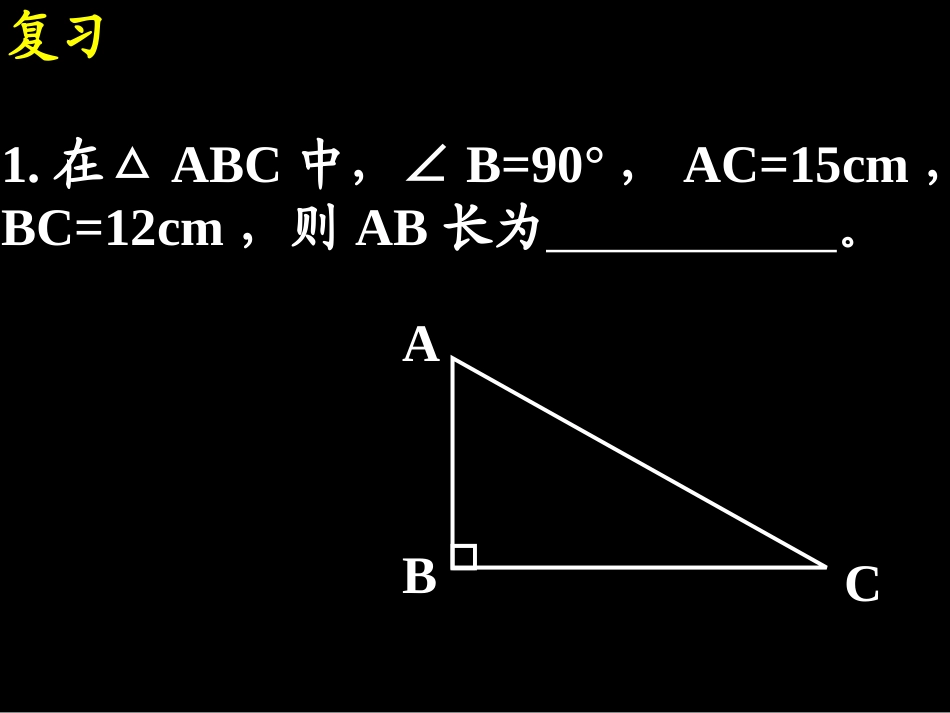
14.1勾股定理（3）---勾股定理的拓展训练复习勾股定理：如果直角三角形的两直角边长分别为a，b，斜边长为c，那么a2+b2=c2.ABCcba复习1.在△ABC中，∠B=90°，AC=15cm，BC=12cm，则AB长为。ABC范例例1.在Rt△ABC中，∠C=90°，BC=12cm，S△ABC=30cm2，求边AB的长。ABC12S=305根据题意画图题求斜边AB边上的高--1.如图，在△ABC中，∠ACB=900，AB=50cm，BC=30cm，CDAB⊥于D，求CD的长。ABCD方法方法11：利用面积相等：利用面积相等练习练习方法方法22：利用勾股定：利用勾股定理理建立建立方程方程复习2.在Rt△ABC中，∠C=90°，a=8，c=17，求△ABC的周长和△ABC的面积。求斜边AB边上的高---巩固3.直角三角形的两条直角边为5cm、12cm，求斜边上的高。ABCD巩固3.在等腰△ABC中，腰AB=10cm，底BC=16cm，求底边BC上的高。ABCDABC3、△ABC中,AB=AC=20cm,BC=32cm.求△ABC面积.D练习练习先构造直角，再用勾股定理巩固5.如图，在△ABC中，AB=15，AC=20，BC边上的高AD=12，求BC的长。CABD6.如图，在△ABC中，AB=15，BC=14，AC=13，求△ABC的面积。ABC151413练习练习D方法：利用勾股定理方法：利用勾股定理建立方建立方程程范例例2.如图，有一块直角三角形纸板ABC，两直角边AC=6cm，BC=8cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且点C落到点E处，求CD的长。CABDE折叠问题DECBA8、已知，在△ABC中，∠C=900，AC=5cm,BC=10cm,将△ABC折叠，使点B与点A重合，折痕为DE.求CD的长度.练习练习巩固6.如图，矩形纸片ABCD的长AD＝9cm，宽AB＝3cm，将其折叠，使点D与点B重合，求折叠后DE和折痕EF的长．DABCEFG小结1．勾股定理的应用2．折叠问题１、课本10页：8、92、课堂练习：4页：148页：8、5、7、9、12、13、（6、11题除外）作业1.如图，在RtABC△中，∠C=90°，点D是BC边上的一点，且BD=AD=10，∠ADC=60°，求△ABC的面积．CABD60°11．如图，在四边形．如图，在四边形ABCDABCD中，∠中，∠BAD=90BAD=9000，∠，∠DBC=90DBC=9000，，AD=3AD=3，，AB=4AB=4，，BC=12BC=12，，求求CDCD；；DABC练习练习2、已知等边三角形ABC的边长是6cm，(1)求高AD的长；(2)S△ABCABCD解：(1)∵△ABC是等边三角形，AD是高在Rt△ABD中,ADB=90∠ADB=90∠00222BDABADcmAD3327936ADBCSABC21)2()(39336212cm321BCBD若等边三角形的边长是a呢？4、在等腰△ABC中，AB＝AC＝13cm，BC=10cm,求△ABC的面积和AC边上的高。ABCD131310H22、利用面积相等、利用面积相等BHACADBC2121练习练习1、先构造直角，再用勾股定理7、如图，∠ACB=∠ABD=90°，CA=CB，∠DAB=30°，AD=8，求AC的长。解：∵∠ABD=90°，∠DAB=30°∴BD=AD=421在Rt△ABD中,根据勾股定理484822222BDADAB在Rt△ABC中，CBCACBCAAB且,222242122222ABCACAAB62AC又AD=8ABCD30°89、如图，在△ABC中，AB=AC，D点在CB延长线上，求证：AD2-AB2=BD·CDABCD证明：过A作AE⊥BC于EE∵AB=AC，∴BE=CE在Rt△ADE中，AD2=AE2+DE2在Rt△ABE中，AB2=AE2+BE2∴AD2-AB2=(AE2+DE2)-(AE2+BE2)=DE2-BE2=(DE+BE)·(DE-BE)=(DE+CE)·(DE-BE)=BD·CD册：2页：15作业3.如图，在△ABC中，∠ACB=90°，AC=，斜边AB在x轴上，点C在y轴的正半轴上，点A的坐标为(2,0)，点8的坐标为(-8,0)，求直角边BC所在直线的解析式．ABCxyO52本节课学习了什么内容？你对学习本节课知识有什么体会?谈一谈谈一谈