一次函数问题的实际应用VIP免费

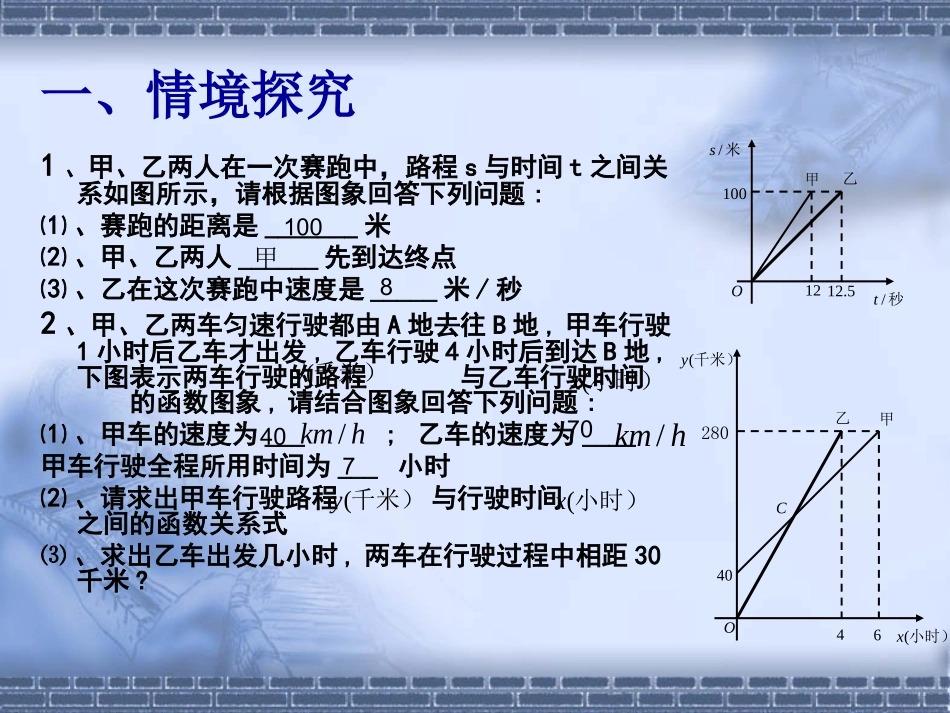
一次函数图象的实际应用一次函数图象的实际应用----------行程问行程问题题实验中学实验中学刘云圣刘云圣教学目标：1、学生通过学习能够将实际问题转化为数学问题，获得建立函数模型解决实际问题的经验和方法。2、能通过一次函数图象反映的信息探究实际问题中的数量关系，体会数形结合思想。3、进一步培养学生发现问题，提出问题，分析问题，解决问题的能力题型概述：是以一次函数图象为载体，构建的具有实际意义的数学问题，其特点是实际问题中的数量及其关系蕴涵在函数图象中，图象有单图象和双图象，类型有行程、工作量、进出等问题。280一、情境探究1、甲、乙两人在一次赛跑中，路程s与时间t之间关系如图所示，请根据图象回答下列问题:⑴、赛跑的距离是_______米⑵、甲、乙两人______先到达终点⑶、乙在这次赛跑中速度是_____米/秒2、甲、乙两车匀速行驶都由A地去往B地,甲车行驶1小时后乙车才出发,乙车行驶4小时后到达B地,下图表示两车行驶的路程与乙车行驶时间的函数图象,请结合图象回答下列问题:⑴、甲车的速度为___;乙车的速度为____甲车行驶全程所用时间为___小时⑵、请求出甲车行驶路程与行驶时间之间的函数关系式⑶、求出乙车出发几小时,两车在行驶过程中相距30千米?O米/s秒/t乙甲5.1210012O千米）(y千米）(y千米）(y小时）(x小时）(x小时）(xhkm/4046100C甲乙hkm/甲840707归纳总结:1、看图、识图：结合文字部分找出已知信息，横、纵轴所表达的意义，再依次提取每个点所蕴涵的信息。2、用图：用图象提供的信息，列算式、方程、解析式解决问题。二、合作交流一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，设慢车行驶的时间为小时，两车之间的距离为，图中折线表示与之间的函数关系，请同学们根据图象进行以下探究：⑴、甲、乙两地之间的距离为_____⑵、请解释图中点B的实际意义⑶、求线段BC所表示的与之间的函数关系式⑷、若第二列快车也从甲地出发驶向乙地，速度与第一列快车相同，在第一列快车与慢车相遇30分钟后，第二列快车与慢车相遇，求慢车出发多少小时后第二列快车出发？xyxkmxykmy/900ADCBO12hx/4千米）(y900解:1、由图象可知:900km2、B点的实际意义是快车与慢车行驶4小时相遇3、两车速度和为：900÷4=225km/h慢车速度为：900÷12=75km/h快车速度为：225－75=150km/h快车到达乙地时慢车行驶的路程：75×6=450km∴C(6,450)设=（）把（4，0）（6，450）代入得解得∴=4、设慢车出发t小时后第二列快车出发，由题意可知：75x4.5+150(4.5－t)=900解得:t=0.75答:慢车出发0.75小时后第二列快车出发yBCyBCbkx0k900225bk044506bkbk225900(46)xxB三、变式训练一列快车从甲地匀速驶往乙地，一列慢车从乙地匀速驶往甲地，两车同时出发。不久，第二列快车也从甲地发往乙地，速度与第一列快车相同。在第一列快车与慢车相遇30分钟后，第二列快车与慢车相遇。设慢车行驶时间为小时，慢车与第一列快车之间的距离、慢车与第二列快车之间的距离与之间的函数关系如图1、图2所示，根据图象信息解答下列问题：⑴甲、乙两地之间的距离为____千米;慢车速度为____;C点坐标为（）⑵求图1中线段CD所表示的与之间的函数关系式⑶图2中t的实际意义是什么？求出t的值：hx/1yxx9009002/ykm1/ykmA12hx/12OOCDD1图2图1(y千米）小时）(xhkm/45.4t6t2y（千米）解:⑴、900慢车速度为：75C(6,450)⑵、设=()把(6,450)(12,900)代入=中得：解得∴⑶、由题意可知：75x4.5+150(4.5－t)=900解得:t=0.75hkm/yCDbkx450690012bkbk075bkbkxyCD)126(75xxy为常数、bkk,0四、课堂小结:五、当堂检测:一辆快车从甲地开往乙地，一辆慢车从乙地开往甲地，两车同时出发，设慢车离乙地的距离为,快车离乙地的距离为,慢车行驶时间为,两车之间的距离为,、与的函数关系图象如图1所示，与的函数关系图象如图2所示:1、图中的=______,=______:2、求线段BC所表示的函数关系式)(kmy1)(kmy2)(kms)(hx600Ob610ABCDy1y2x)(hxabsx2图1图)(kmy)(hx600Oa10)(kms解：1、a=6b=2、慢车速度为：600÷10=60km/h快车到达乙地时慢车行驶的路程为：60...