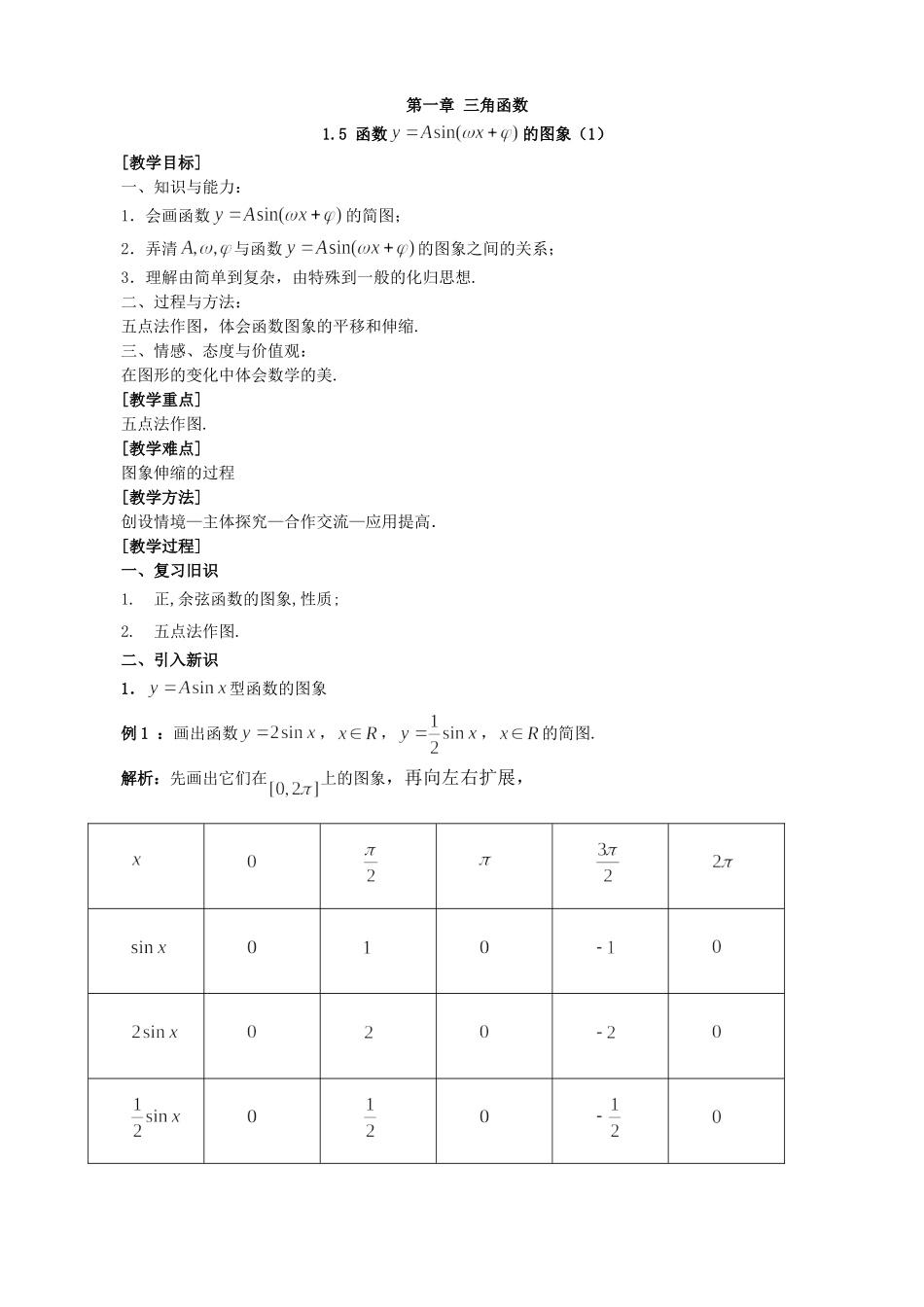
第一章三角函数1.5函数的图象(1)[教学目标]一、知识与能力:1.会画函数的简图;2.弄清与函数的图象之间的关系;3.理解由简单到复杂,由特殊到一般的化归思想.二、过程与方法:五点法作图,体会函数图象的平移和伸缩.三、情感、态度与价值观:在图形的变化中体会数学的美.[教学重点]五点法作图.[教学难点]图象伸缩的过程[教学方法]创设情境—主体探究—合作交流—应用提高.[教学过程]一、复习旧识1.正,余弦函数的图象,性质;2.五点法作图.二、引入新识1.型函数的图象例1:画出函数,,,的简图.解析:先画出它们在上的图象,再向左右扩展,由图可知,对于同一个,,的图象上的点的纵坐标等于,的图象上的点的纵坐标的倍,因此,,的图象可以看作正弦曲线上所有点的纵坐标伸长到原来的倍(横坐标不变的情况下)而得到的。,的图象的情况也类似:纵坐标变为原来的(横坐标不变情况下).总结:一般地,函数,的图象可看作把正弦曲线上所有点的纵坐标伸长(时)或缩短(时)到原来的倍(横坐标不变的情况下)而得到,因此,,的值域是,最大值为,最小值为.2.型函数的图象例2:画出函数,,,的函数简图。解析:先画出它们在一个周期内的图象,再向左、右扩展,xyO––32222sinyxsinyx1sin2yxxyO24211––总结:一般地,函数,()的图象可以看作把正弦曲线上所有点的横坐标缩短(时)或伸长(时)到原来的倍(纵坐标不变的情况下)而得到的.3.型的函数图象例3:画出函数,,,的简图.解析:由函数图象的平移知:,的图象可看作,的图象向左平移个单位得到;,的图象可看作,的图象向右平移个单位得到。可得图象如下:总结:一般地,函数(),的图象,可看作把正弦曲线上所有点向左(时)或向右(时)平行移动个单位而得到.三、巩固探究练习:画出下列函数在长度为一个周期的闭区间上的简图(五点法).(1),;(2),.四、小结作业1、小结:1.型函数的图象;2.型函数的图象;yO294537643543.型函数的图象.2、作业:课本P55练习1;课本P58习题1.5A组21.5函数的图象(2)[教学目标]一、知识与能力:1.明确函数中的物理意义及它们对函数的图象各有什么影响;2.逐步掌握由,的图象,通过图象的伸缩平移变换得到函数,的图象的方法.二、过程与方法:体会数学中的代换思想及化归的方法.三、情感、态度与价值观:体验数学知识的内部联系.[教学重点]的性质和图象.[教学难点]函数图象的伸缩、平移变换.[教学方法]创设情境—主体探究—合作交流—应用提高.[教学过程]一、复习旧识1.及的图象与性质;2.五点法作图;3.复习的图象与性质(1)函数的图象与的图象有什么关系?(2)函数的图象与的图象有什么关系?(3)函数的图象与的图象有什么关系?二、引入新识1.的物理意义当,(其中,)表示一个振动量时,表示这个量振动时离开平衡位置的最大距离,通常称为这个振动的振幅,往复振动一次需要的时间称为这个振动的周期,单位时间内往复振动的次数,称为振动的频率.称为相位,时的相位称为初相.2.图象的变换例题:画出函数的简图.解析:函数的周期为,先画出它在长度为一个周期内的闭区间上的简图,再左右拓展即可.先用五点法画图:函数的图象可看作由下面的方法得到的:①图象上所有点向左平移个单位,得到的图象上;②再把图象上所点的横坐标缩短到原来的,得到的图象;③最后把图象上所有点的纵坐标伸长到原来的倍,得到的图象.总结:一般地,函数,的图象(其中,)的图象,可看作由下面的方法得到:①把正弦曲线上所有点向左(当时)或向右(当时)平行移动个单位长度;②再把所得各点横坐标缩短(当时)或伸长(当时)到原来的倍(纵坐标不变);③再把所得各点的纵坐标伸长(当时)或缩短(当时)到原来的倍(横坐标不变).xyO36532sin()3yxsin(2)3yxsinyx即先作相位变换,再作周期变换,再作振幅变换。思考:以上步骤能否变换次序?因为,所以,函数的图象还可看作由下面的方法得到的:①图象上所点的横坐标缩短到原来的,得到函数的图象;②再把函数图象上所有点向左平移个单位,得到函数的图象;③再把...