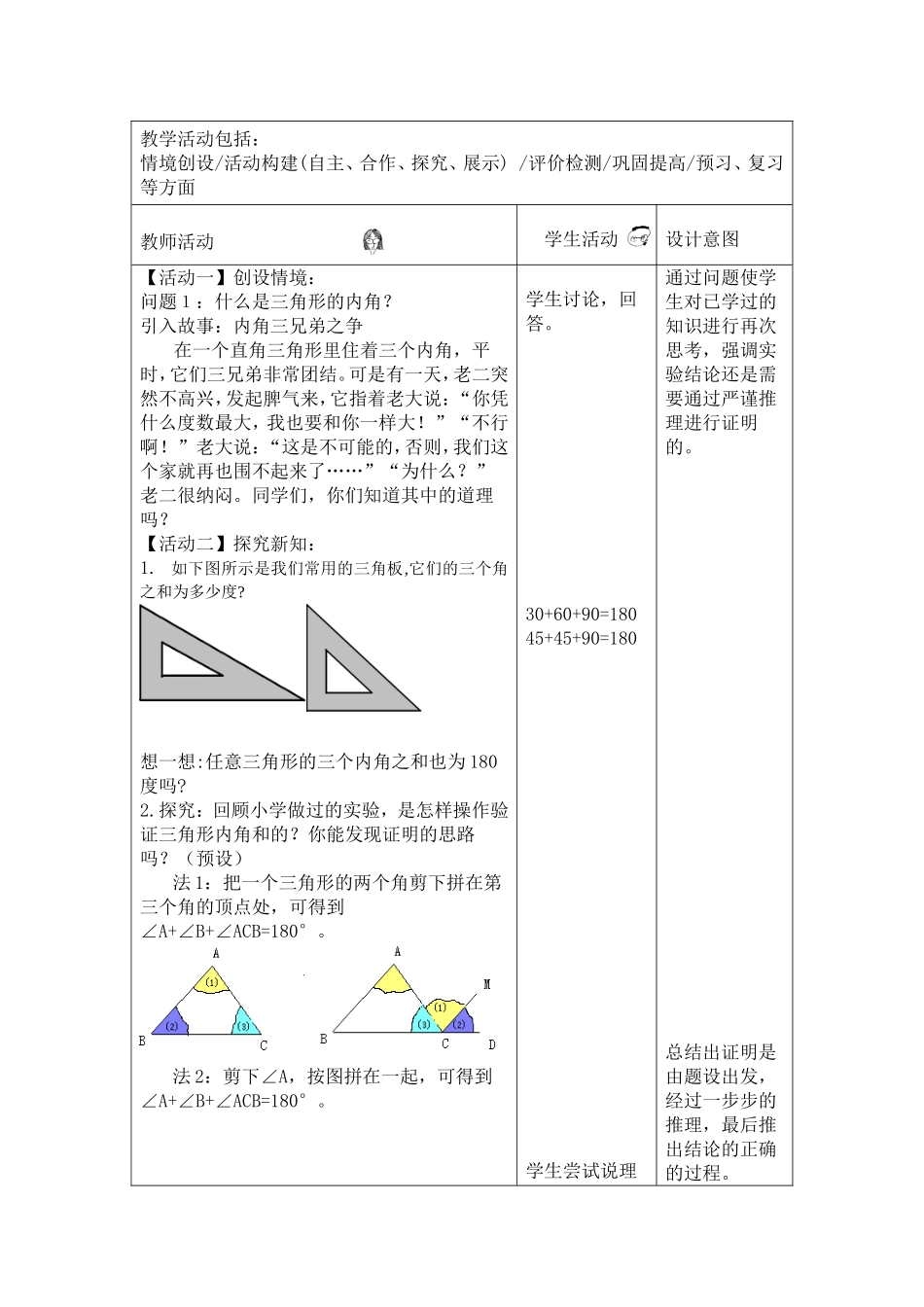
11.2.1三角形的内角教学设计课题11.2.1三角形的内角授课年级初一学科数学课时安排1授课日期2017.5教学目标知识与技能理解和掌握三角形的内角和性质数学能力目标经历对三角形内角和进行实验、猜测、说理证实的数学研究过程,初步体验感受数学探索、发现的科学历程数学思想方法目标体会直观感知与理性思考的联系和区别,懂得直观结论需要说理证实的意义,体会化归、特殊到一般的数学思想和方程的思想教学背景分析教学重点了解三角形的内角和的性质,学会解决简单的实际问题。教学难点说明三角形内角和等于180°的性质。学情分析三角形内角和学生小学已经接触过,本节课可以让学生通过动手操作自主探究论证得出三角形内角和是180°。教学方法探究法、讨论法教具学具学案、三角板、自制教具辅助媒体PPT教学结构(思路)设计【活动一】创设情境【活动二】探究新知【活动三】应用新知【活动四】例题讲解【活动五】课堂小结【活动六】布置作业教学活动设计教学活动包括:情境创设/活动构建(自主、合作、探究、展示)/评价检测/巩固提高/预习、复习等方面教师活动学生活动设计意图【活动一】创设情境:问题1:什么是三角形的内角?引入故事:内角三兄弟之争在一个直角三角形里住着三个内角,平时,它们三兄弟非常团结。可是有一天,老二突然不高兴,发起脾气来,它指着老大说:“你凭什么度数最大,我也要和你一样大!”“不行啊!”老大说:“这是不可能的,否则,我们这个家就再也围不起来了……”“为什么?”老二很纳闷。同学们,你们知道其中的道理吗?【活动二】探究新知:1.如下图所示是我们常用的三角板,它们的三个角之和为多少度?想一想:任意三角形的三个内角之和也为180度吗?2.探究:回顾小学做过的实验,是怎样操作验证三角形内角和的?你能发现证明的思路吗?(预设)法1:把一个三角形的两个角剪下拼在第三个角的顶点处,可得到∠A+∠B+∠ACB=180°。法2:剪下∠A,按图拼在一起,可得到∠A+∠B+∠ACB=180°。学生讨论,回答。30+60+90=18045+45+90=180学生尝试说理通过问题使学生对已学过的知识进行再次思考,强调实验结论还是需要通过严谨推理进行证明的。总结出证明是由题设出发,经过一步步的推理,最后推出结论的正确的过程。法3:把和剪下按图拼在一起,可得到∠A+∠B+∠ACB=180°。已知:△ABC求证:∠A+∠B+∠C=180°证明:法1:过点C作CM∥AB,则∠A=∠ACM,∠B=∠DCM,又∵∠ACB+∠ACM+∠DCM=180°∴∠A+∠B+∠ACB=180°即:三角形的内角和等于180°。由图2、图3你又能想到什么证明方法?请说说证明过程。三角形内角和定理:三角形三个内角的和等于180°。【活动三】应用新知1.(口答)下列各组角是同一个三角形的内角吗?为什么?(1)3°,150°,27°(2)60°,40°,90°(3)30°,60°,50°2.(1)在△ABC中,∠A=35°,∠B=43°则∠C=.(2)在△ABC中,∠A:∠B:∠C=2:3:4则∠A=∠B=∠C=.【活动四】例题讲解例:如图,已知:△ABC中,BD、CE分别是△ABC的两条角平分线,相交于点O.(1)当∠ABC=60°,∠ACB=80°时,求∠BOC的度数;(2)当∠A=40°时,求∠BOC的度数;证明。学生归纳得出三角形内角和定理。学生思考,分析,尝试解决。学生讨论,回答,课堂展示通过实际生活中的问题让学生体会到数学与生活的密切联系,激发学生的学习兴趣和回答问题的积极性,进一步熟练应用三角形的内角和解决问题。通过练习巩固三角形内角和的运用。当∠A=x°时,求∠BOC的度数(用含x代数式表示);(3)当∠A=x°时,求∠BOC的度数(用含x代数式表示)【活动五】课堂小结:本节课收获了哪些知识?三角形内角和为180°。【活动六】布置作业:1.思考:(1)一个三角形中最多有个直角?为什么?(2)一个三角形中最多有个钝角?为什么?(3)一个三角形中至少有个锐角?为什么?(4)任意一个三角形中,最大的一个角的度数至少为.2.校本作业半张学生进行归纳总结,畅谈本节课的收获。通过归纳总结进一步构建完整的知识体系。