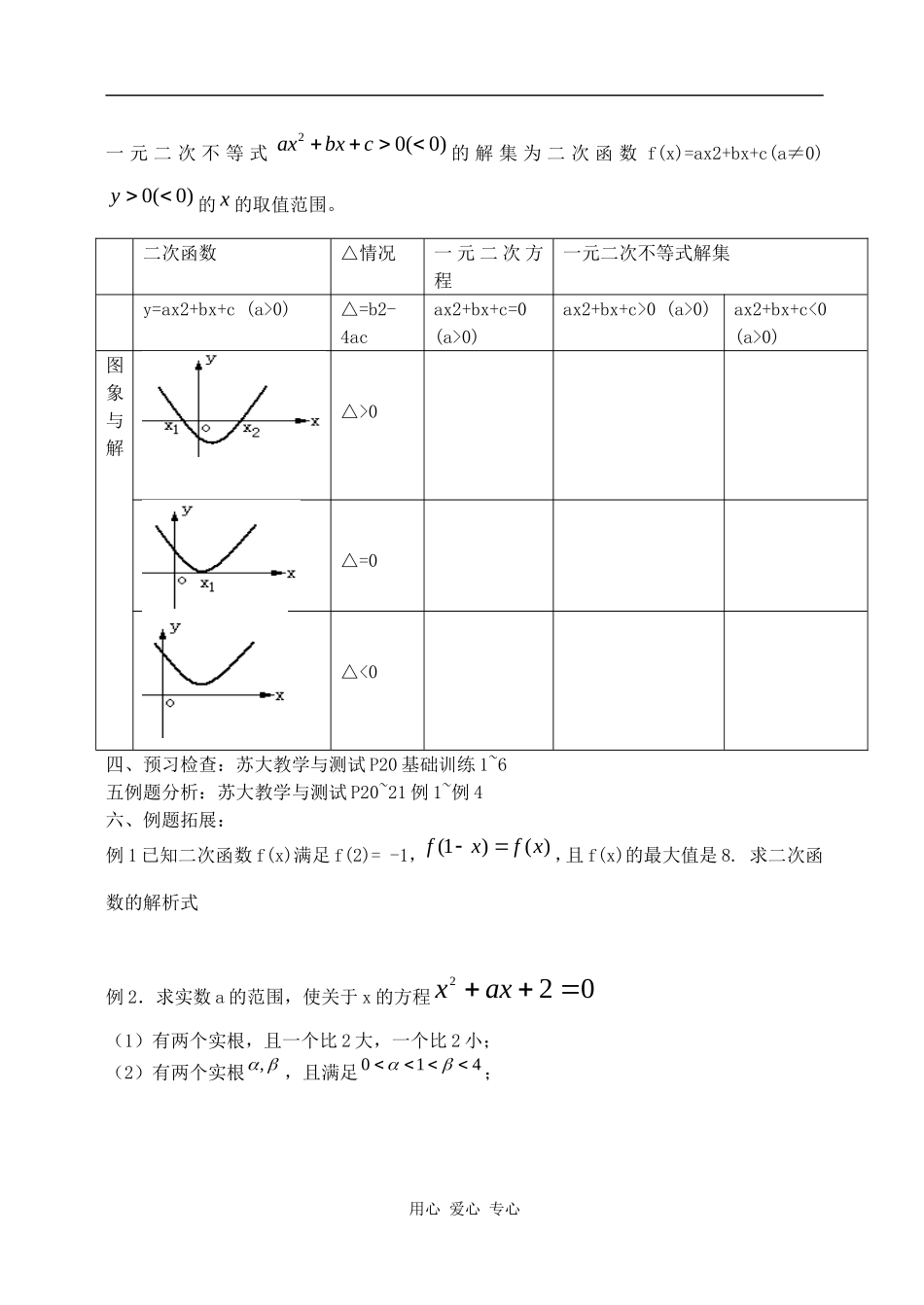
二、函数与导数10二次.函数一、考纲要求二、命题规律1.二次函数是历年高考的重点,常与导数、一元二次方程根的分布、一元二次不式综合考查。在填空题和解答题中都会出现。一般为中档题或难题。2.二次函数的解析式、图象及其性质是解题的重要基础。配方法是解题关键。3.解题中常运用分类讨论思想和数形结合的思想。三、要点回顾:1.二次函数的解析式的三种形式(求一个二次函数的解析式需三个独立条件)(1)一般式:f(x)=ax2+bx+c(a≠0),其中a是决定,c是,而ba是决定。(2)顶点式(配方式):f(x)=a(x-h)2+k其中是抛物线的顶点坐标。(3)两根式(因式分解):f(x)=a(x-x1)(x-x2),其中x1,x2是抛物线与2.二次函数f(x)=ax2+bx+c(a≠0)的图象是一条抛物线,对称轴,顶点坐标(1)a>0时,抛物线开口向上,函数在(,]2ba上单调,在[,)2ba上单调,(2)a<0时,抛物线开口向下,函数在(,]2ba上单调,在[,)2ba上单调,3.二次函数f(x)=ax2+bx+c(a≠0)当240bac时图象与x轴有两个交点M1(x1,0),M2(x2,0)21MM4.(1)二次函数与一元二次方程关系方程20(0)axbxca的根为二次函数f(x)=ax2+bx+c(a≠0)0y的x的取值。(2)二次函数与一元二次不等式的关系用心爱心专心内容要求二次函数ABC√一元二次不等式20(0)axbxc的解集为二次函数f(x)=ax2+bx+c(a≠0)0(0)y的x的取值范围。二次函数△情况一元二次方程一元二次不等式解集y=ax2+bx+c(a>0)△=b2-4acax2+bx+c=0(a>0)ax2+bx+c>0(a>0)ax2+bx+c<0(a>0)图象与解△>0△=0△<0四、预习检查:苏大教学与测试P20基础训练1~6五例题分析:苏大教学与测试P20~21例1~例4六、例题拓展:例1已知二次函数f(x)满足f(2)=-1,(1)()fxfx,且f(x)的最大值是8.求二次函数的解析式例2.求实数a的范围,使关于x的方程022axx(1)有两个实根,且一个比2大,一个比2小;(2)有两个实根,,且满足410;用心爱心专心例3.对于任意2m,函数2()21fxmxxm恒负,求x的取值范围。七、巩固练习:苏大教学与测试P21巩固练习1~4八、课堂小结:九、作业布置:苏大教学与测试自我测试B10二次函数十、课后反思10.二次函数班级:姓名学号评价1.函数234xxyx的定义域为2.已知为常数,若22()43,()1024,fxxxfaxbxx则5a-b=3.若函数2()412fxaxbxcfff满足()(),那么()与f(3)的大小关系为4.二次函数()22fxfxfxfx满足()(),又()在0,2上是增函数,且与f(a)f(0),则实数a的取值范围是5.函数2sin1sinyxaxa(),当时有最小值,当sinx=1时有最大值,则实数a的取值范围是6.已知222228Rxyxxyx,y,且,则的最大值是,最小值是7.已知函数210142afxxax()在区间,上的最小值是-2,则实数a=8.若二次函数2222111pxpp2f(x)=4x()在区间,内至少存在一点c,使得f(c)>0,则实数p的取值范围是9.设213242fxxxkkRk()(,),问是否存在实数m,n(m