4.3--三角函数的图象与性质VIP免费

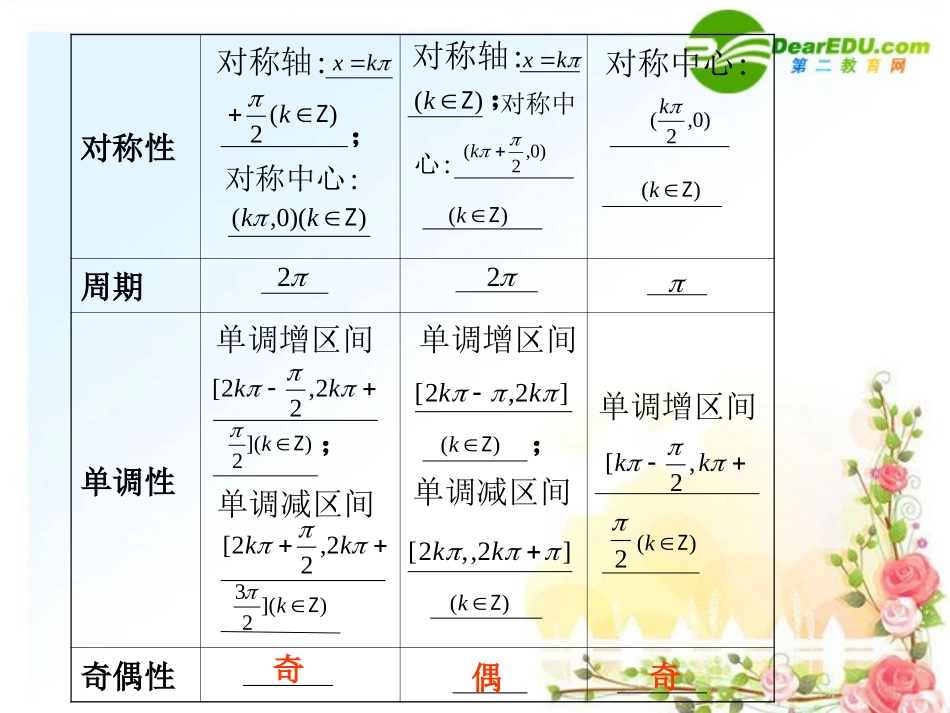
§4.3三角函数的图象与性质要点梳理1.“五点法”作图原理:在确定正弦函数y=sinx在［0，2］上的图象形状时,起关键作用的五个点是、、、、.余弦函数呢？(0,0))1,2()0,()1,23()0,2(基础知识自主学习2.三角函数的图象和性质:y=sinxy=cosxy=tanx定义域图象值域R函数性质[-1,1][-1,1]RR,2|{kxx(k∈Z)对称性周期单调性奇偶性:对称轴kx)(2Zk；:对称中心))(0,(Zkk:对称轴kx)(Zk；对称中:心kk2,22[)(Zk:对称中心)(Zk22单调增区间)](2Zk；单调减区间kk2,22[)](23Zk单调增区间]2,2[kk)(Zk；单调减区间]2,,2[kk)(Zk单调增区间kk,2[2)(Zk奇奇偶)0,2(k)0,2(k3.一般地对于函数f（x）,如果存在一个不为0的常数T，使得当x取定义域内的每一个值时,都有f（x+T）=f（x），那么函数f（x）就叫做周期函数，非零常数T叫做这个函数的周期，把所有周期中存在的最小正数,叫做最小正周期(函数的周期一般指最小正周期).函数y=Asin(x+）或y=Acos（x+）（>0且为常数）的周期函数y=Atan(x+)(>0)的周期,2T.T基础自测1.函数y=1-2sinxcosx的最小正周期为（）解析4.D2.C.B21.A.22,2sin1TxyB2.设点P是函数f(x)=sinx(≠0)的图象C的一个对称中心,若点P到图象C的对称轴的距离的最小值是则f(x)的最小正周期是（）解析由正弦函数的图象知对称中心与对称轴的距离的最小值为最小正周期的故f（x）的最小正周期为T=,44.D2.C.B2.A,41.44B3.函数y=sin的图象（）A.关于点对称B.关于直线对称C.关于点对称D.关于直线对称解析验证法：)32(x)0,3(4x)0,4(3x.)0,3()32sin(,0sin)332sin(,3对称的图象关于点所以时当xyxA4.在下列函数中,同时满足以下三个条件的是()①在上递减；②以为周期；③是奇函数.A.y=tanxB.y=cosxC.y=-sinxD.y=sinxcosx解析y=tanx的周期为，故A错.y=cosx为偶函数，故B错.y=sinxcosx=sin2x的周期为，故D错.y=-sinx的周期为2,是奇函数，由图象知在上是递减函数，故C正确.)2,0(221)2,0(C5.（2009·四川）已知函数f(x)=sin(x∈R)，下面结论错误的是（）A.函数f(x)的最小正周期为2B.函数f(x)在区间上是增函数C.函数f(x)的图象关于直线x=0对称D.函数f(x)是奇函数解析A正确;由图象知y=-cosx关于直线x=0对称，C正确.y=-cosx是偶函数，D错误.)2(x2,0,2,cos)2sin(Txxy;B,2,0cos,2,0cos正确增函数上是在上是减函数在xyxyD题型一与三角函数有关的函数定义域求下列函数的定义域：（1）y=lgsin(cosx);(2)y=本题求函数的定义域:(1)需注意对数的真数大于零，然后利用弦函数的图象求解；(2)需注意偶次根式的被开方数大于或等于零，然后利用函数的图象或三角函数线求解.解(1)要使函数有意义,必须使sin(cosx)>0. -1≤cosx≤1,∴0