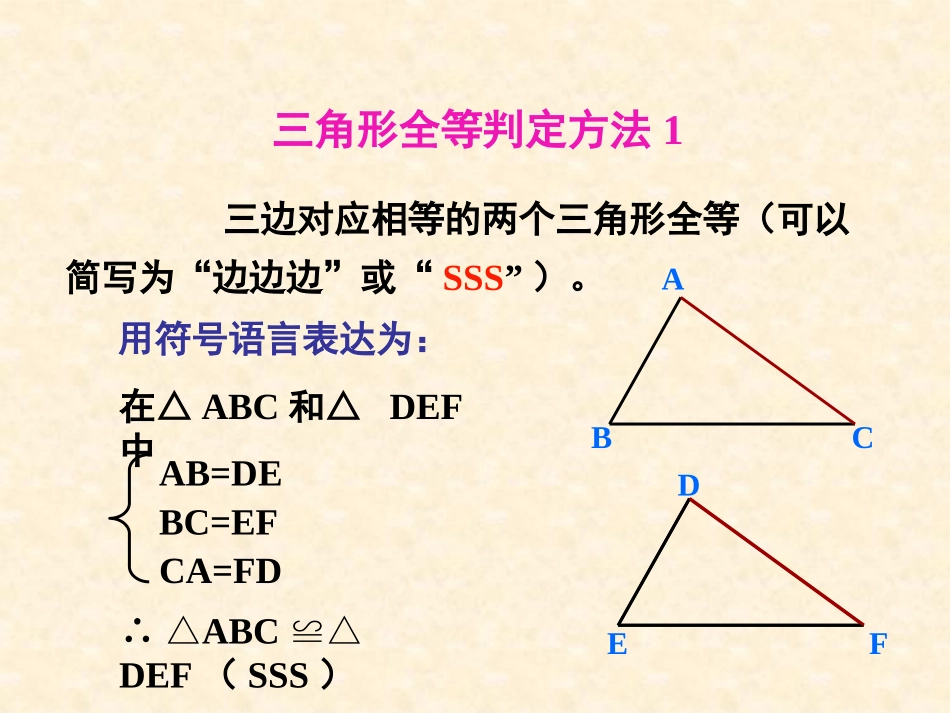
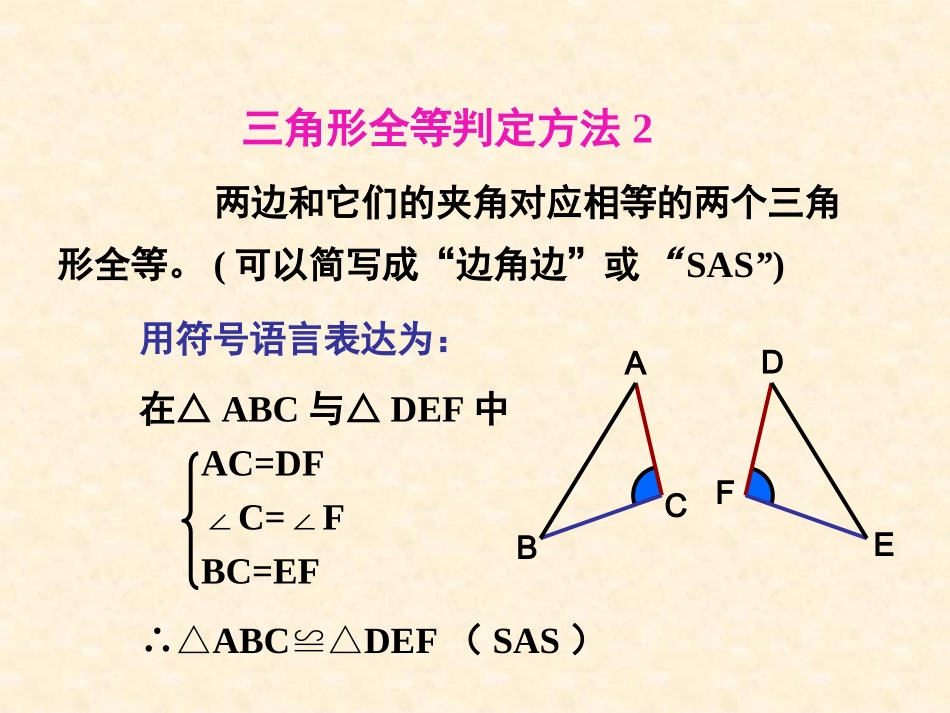
§12.2三角形全等的判定(三)三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”)。ABCDEF在△ABC和△DEF中∴△ABC≌△DEF(SSS)AB=DEBC=EFCA=FD用符号语言表达为:三角形全等判定方法1三角形全等判定方法2用符号语言表达为:在△ABC与△DEF中∴△ABCDEF≌△(SAS)两边和它们的夹角对应相等的两个三角形全等。(可以简写成“边角边”或“SAS”)FEDCBAAC=DF∠C=F∠BC=EFDCBAABDABCABDABCSSA不能判定全等1.若AB=AC,则添加一个什么条件可得△ABDACD?≌△△ABDACD≌△AB=ACABDC∠BAD=CAD∠SASAD=ADBD=CDS2.如图,要证△ACBADB≌△,至少选用哪些条件可ABCD△ACBADB≌△SAS证得△ACBADB≌△AB=AB∠CAB=DAB∠AC=ADSBC=BD?继续探讨三角形全等的条件:两角一边思考:已知一个三角形的两个角和一条边,那么两个角与这条边的位置上有几种可能性呢?ABC图1在图1中,边AB是∠A与∠B的夹边,我们称这种位置关系为两角夹边观察下图中的△ABC,画一个△ABC,使AB=AB,∠A=∠A,∠B=B∠结论:两角及夹边对应相等的两个三角形全等(ASA).′′′′′′′观察:△ABC与△ABC全等吗?怎么验证?画法:1.画AB=AB;2.在AB的同旁画∠DAB=∠A,∠EBA=∠B,AD、BE交于点C′′′′′′′′′ACBA′EDCB′′′思考:这两个三角形全等是满足哪三个条件?′′′′′如何用符号语言来表达呢?证明:在△ABC与△ABC中∠A=A∠AB=AB∴△ABCA’B’C’≌△(ASA)ACBA′CB′′′′′′′′∠B=B∠′两角及夹边对应相等的两个三角形全等(ASA).两角和它们的夹边对应相等的两个三角形全等,简写成“角边角”或“ASA”。(ASA)下列条件能否判定△ABCDEF.≌△(1)∠A=EAB=EFB=D∠∠∠试一试请先画图试试看如图,小明不慎将一块三角形模具打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗?如果可以,带哪块去合适?你能说明其中理由吗?AB利用“角边角定理”可知,带B块去,可以配到一个与原来全等的三角形玻璃。CBEAD考考你1、如图,已知AB=DE,∠A=D∠,,B=E∠∠,则△ABCDEF≌△的理由是:ABCDEF角边角(ASA)例1、如图,AB=AC,∠B=∠C,那么△ABE和△ACD全等吗?为什么?证明:在△ABE与△ACD中∠B=C∠(已知)AB=AC(已知)∠A=A∠(公共角)∴△ABEACD≌△(ASA)AEDCB例2.如图,O是AB的中点,=,与全等吗?为什么?ABAOCBODOABCD两角和夹边对应相等练习1已知:如图,AB=A′C,∠A=∠A′,∠B=C∠求证:△ABE≌△A′CD________()________()________()证明:在和中∴△________≌△()CDA'ABE∠A=A’∠已知AB=A’C已知∠B=C∠已知ABEA’CDASA△ABEA’CD△1、如图:已知AB∥DE,AC∥DF,BE=CF。求证:△ABCDEF≌△。ABCDEF考考你证明:∵BE=CF(已知)∴BC=EF(等式性质)∠B=E∠在△ABC和△DEF中BC=EF∠C=F∠∴△ABCDEF≌△(ASA)∵ABDEACDF∥∥(已知)∴∠B=DEF,ACB=F∠∠∠判定三角形全等你有哪些方法?(ASA)(SAS)(SSS)ABCDEF1、如图∠ACB=∠DFE,BC=EF,那么应补充一个条件-------------------------,才能使△ABC≌△DEF(写出一个即可)。∠B=∠E或AC=DF你能行吗?(ASA)(SAS)AB=DE可以吗?×ABDE∥∠A=D∠(已知)AB=DE(已知)∠B=E∠(已知)在△ABC和△DEF中∴△ABCDEF≌△(ASA)有两角和它们夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”)。用符号语言表达为:FEDCBA三角形全等判定方法3知识梳理:(1)两角和它们的夹边对应相等的两个三角形全等.简写成“角边角”或“ASA”.知识要点:(2)探索三角形全等是证明线段相等(对应边相等),角相等(对应角相等)等问题的基本途径。数学思想:要学会用分类的思想,转化的思想解决问题。