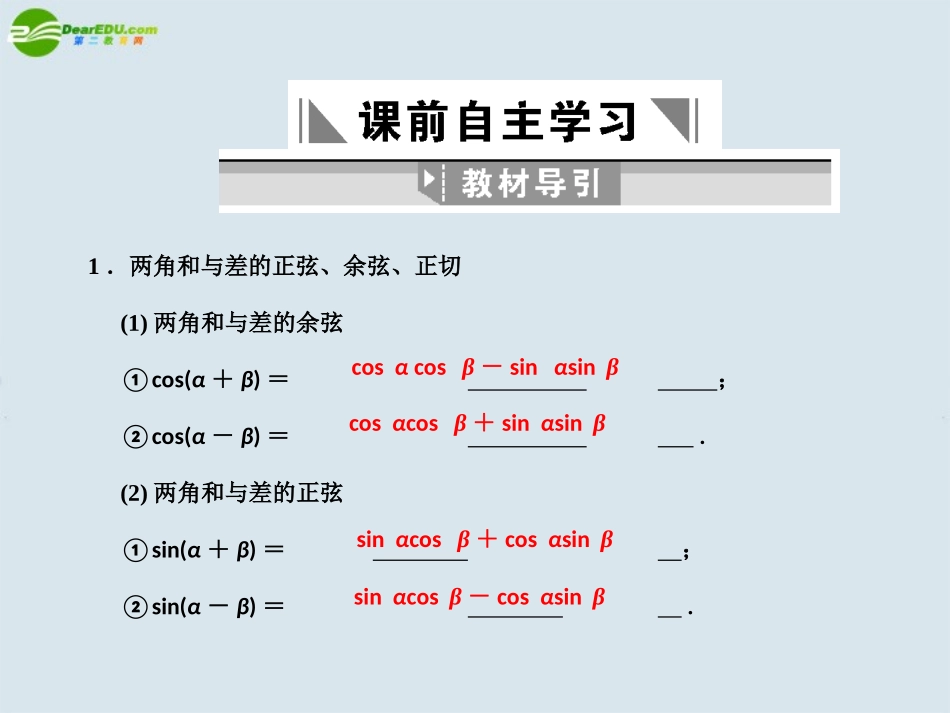
【考纲下载】1.会用向量的数量积推导出两角差的余弦公式.2.能利用两角差的余弦公式导出两角差的正弦、正切公式.3.能利用两角差的余弦公式导出两角和的正弦、余弦、正切公式,导出二倍角的正弦、余弦、正切公式,了解它们的内在联系.第5讲两角和与差的三角函数1.两角和与差的正弦、余弦、正切(1)两角和与差的余弦①cos(α+β)=;②cos(α-β)=.(2)两角和与差的正弦①sin(α+β)=;②sin(α-β)=.cosαcosβ-sinαsinβcosαcosβ+sinαsinβsinαcosβ+cosαsinβsinαcosβ-cosαsinβ(3)两角和与差的正切①tan(α+β)=;②tan(α-β)=.(α,β,α+β,α-β均不等于kπ+,k∈Z)提示:(1)和(差)角的正弦、余弦公式不能按分配律展开,如sin(α+β)≠sinα+sinβ,cos(α-β)≠cosα-cosβ;(2)两角和与差的正弦、余弦公式均为恒等式,对任意的角α、β均成立.2.倍角公式及其变形(1)sin2α=,cos2α==2cos2α-1=1-2sin2α,tan2α=.(2)cos2α=,sin2α=.1+cosα=,1-cosα=.2sinαcosαcos2α-sin2α提示:用tan表示sinα、cosα:sinα=2sincos=cosα=cos2-sin2=1.sin15°cos75°+cos15°sin105°等于()A.0B.C.D.1解析:sin15°cos75°+cos15°sin105°=sin15°cos75°+cos15°sin75°=sin(15°+75°)=sin90°=1.答案:D2.已知x∈cosx=则tan2x=()A.-B.C.D.解析: x∈cosx=∴sinx=∴tanx=∴tan2x=答案:A3.设α∈若sinα=则等于()解析: α∈且sinα=∴cosα=∴cos=(cosα-sinα)=cosα-sinα=答案:B4.函数f(x)=sinx+sin的最大值是________.解析: f(x)=sinx+cosx=2sin∴f(x)max=2.答案:2直接利用公式化简、求值是常见的,但逆用和变形应用常考常新,它更能开拓思路,培养从正向思维向逆向思维转化的能力,对于公式tan(α+β)=应注意两种变形:tanα+tanβ=tan(α+β)·(1-tanαtanβ)和1-tanα·tanβ=这些都是在解题中经常用到的.求(1+tan21°)(1+tan22°)(1+tan23°)(1+tan24°)的值.思维点拨:由tan(21°+24°)=可得.解: (1+tan21°)(1+tan24°)=1+tan21°+tan24°+tan21°tan24°=1+tan45°(1-tan21°tan24°)+tan21°tan24°=2.同理可求(1+tan22°)(1+tan23°)=2.故(1+tan21°)(1+tan22°)(1+tan23°)(1+tan24°)=4.【例1】变式1:求值coscoscos解:原式=三角函数的求值问题的重要思想方法技巧是沟通已知式与待求式之间的联系,常常对角进行变换,变换时应注意各角之间的和、差、倍、半的关系,常用的角的变换式有:(1)α=(α-β)+β=(α+β)-β;(3)2α=(α+β)+(α-β);【例2】设cossin且<α<π,0<β<求cos的值.思维点拨:由于再由角的范围求出sin及cos即可.解: <α<π,0<β<,∴sin(α-)coscos∴sin=cos=coscos+sin·sin又cos已知α∈cos解: α-+β=α+β+变式2:求sin(α+β)的值.∴sincos∴sin(α+β)=-cos=-cos1.由已知条件先求所求角的三角函数值,具体选用哪个三角函数,一般由条件中的函数去确定.若已知正切函数值时,选正切函数;若已知正、余弦函数值时,选余弦函数.2.根据角的范围写出所求的角.解: A、B为锐角,sinA=sinB=∴cosA=cosB=∴cos(A+B)=cosAcosB-sinAsinB 0