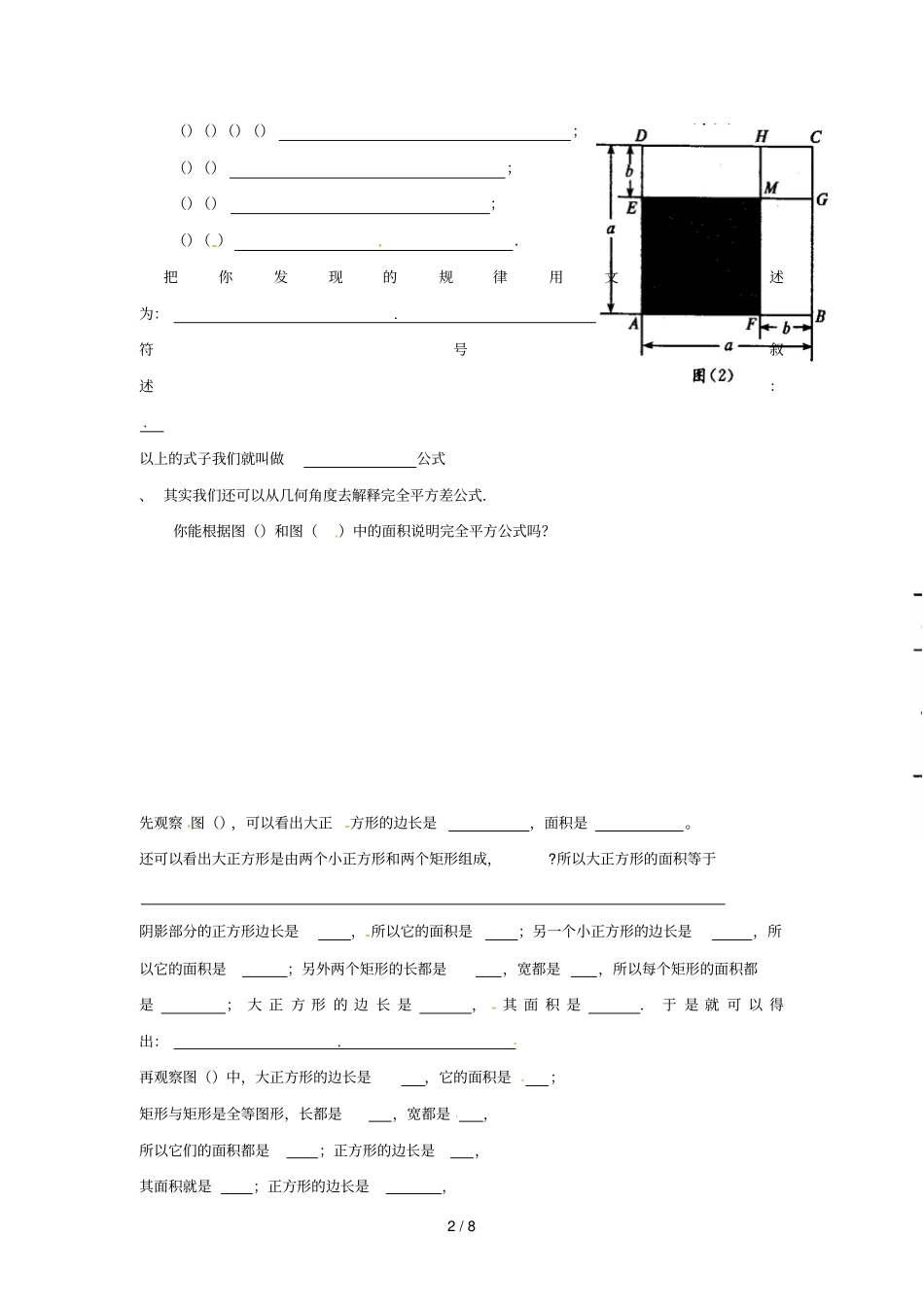
1/8完全平方公式【学习目标】.完全平方公式的推导及其应用;完全平方公式的几何解释..经历探索完全平方公式的过程,进一步发展符号感和推理能力.【学习重点】完全平方公式的推导过程、结构特点、几何解释,灵活应用.【学习难点】理解完全平方公式的结构特征并能灵活应用公式进行计算.【学习过程】一、知识链接:、叙述平方差公式的内容及用字母表示:,.2、用简便方法计算:()97()1002、请同学们自编一个符合平方差公式结构的计算题,并算出结果。二、自主学习:阅读—、计算下列各式,你能发现什么规律?()()()();()();2/8()()()();()();()();()().把你发现的规律用文字叙述为:.符号叙述:.以上的式子我们就叫做公式、其实我们还可以从几何角度去解释完全平方差公式.你能根据图()和图()中的面积说明完全平方公式吗?先观察图(),可以看出大正方形的边长是,面积是。还可以看出大正方形是由两个小正方形和两个矩形组成,?所以大正方形的面积等于阴影部分的正方形边长是,所以它的面积是;另一个小正方形的边长是,所以它的面积是;另外两个矩形的长都是,宽都是,所以每个矩形的面积都是;大正方形的边长是,其面积是.于是就可以得出:.再观察图()中,大正方形的边长是,它的面积是;矩形与矩形是全等图形,长都是,宽都是,所以它们的面积都是;正方形的边长是,其面积就是;正方形的边长是,3/8所以它的面积是.从图中可以看出正方形的面积等于正方形的面积减去两个矩形和的面积再加上正方形的面积。也就是:.这也正好符合完全平方公式.三、学以致用、应用完全平方公式计算:()(4m)()(12)()()()()、运用完全平方公式计算:()()四、课堂巩固:、运用完全平方公式计算:()62x()52y4/8()522x()yx324322、下面各式的计算错在哪里?应当怎样改正?()baba222()baba222五、课堂小结:完全平方公式符号叙述为:.文字叙述为:.六、课后反思:,.(实际用课时)八年级(上)数学讲学稿课题:14.2.1完全平方公式()课型:新课计划课时:【学习目标】1、掌握添括号法则的推导,会综合运用添括号法则、平方差公式、完全平方公式解决问题。2、经历添括号法则的探究,学习逆向思维,经历合作交流,学习根据数学式子的结构特点,5/8适当恒等变形和灵活运用公式【学习重点】添括号法则的推导,知识的综合运用【学习难点】添括号在具体问题中的灵活应用【学习过程】一、知识链接:1、填空:()平方差公式()().(2)完全平方公式ba2ba2.(3)去括号法则:,.2、运用平方差公式计算:(1)yxyx3232()11xyxy()5252bb3、运用完全平方公式计算:(1)322yx()11yxyx()222xx6/8二、探究添括号法则:阅读—.有一些多项式乘多项式,例如:))((cbacba和2)(cba,没有办法直接运用公式,这时候,我们需要把一个多项式看作一个整体,把另外一个多项式看作另外一个整体,这就需要在式子里添加括号。那么如何加括号呢?它有什么法则呢?、去括号:)(cba)(cba.)(cba)(cba.、添括号:acba()acba()acba()acba()、归纳添括号法则:添括号时,如果括号前面是,括到括号里的各项;如果括号前面是,括到括号里的各项.、试一试判断下列运算是否正确,不正确的请改正。())2(222cbacba())23(23banmbanm())232(232yyyy())54()2(542cbacba三、例题应用例.运用乘法公式计算:())32)(32(yxyx()7/8))((cbacba()2)(cba())2)(2(cbacba四、课堂检测、运用乘法公式计算:()2)12(ba())2)(2(zyxzyx())1)(1(yxyx()2)32(yx、计算:()22)72()53(xx()2)2)(2(xx8/8五、能力提高:、计算:、如果,求的值。、如图,一块直径为的圆形钢板,从中挖去直径为与的两个圆,求剩下的钢板的面积。五、课后反思:,