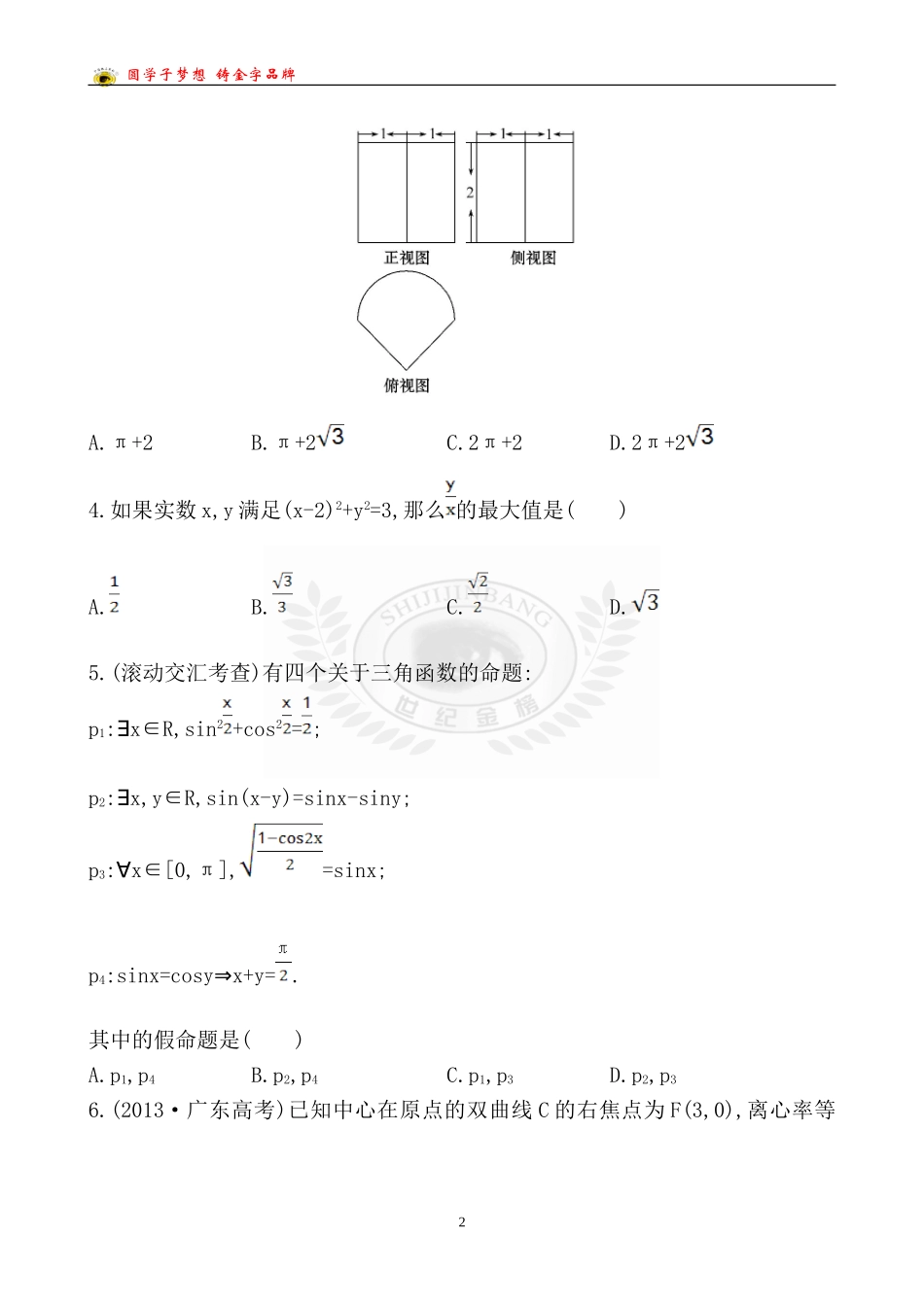
圆学子梦想铸金字品牌温馨提示:此套题为Word版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。关闭Word文档返回原板块。阶段滚动检测(五)第一~八章(120分钟150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(滚动单独考查)满足M{a⊆1,a2,a3,a4},且M∩{a1,a2,a3}={a1,a2}的集合M的个数是()A.1B.2C.3D.42.已知圆C与直线x-y=0及x-y-4=0都相切,圆心在直线x+y=0上,则圆C的方程为()A.(x+1)2+(y-1)2=2B.(x-1)2+(y+1)2=2C.(x-1)2+(y-1)2=2D.(x+1)2+(y+1)2=23.(滚动单独考查)(2014·蚌埠模拟)如图为一个几何体的三视图,正视图和侧视图均为矩形,俯视图中曲线部分为半圆,尺寸如图,则该几何体的体积为()1圆学子梦想铸金字品牌A.π+2B.π+2C.2π+2D.2π+24.如果实数x,y满足(x-2)2+y2=3,那么的最大值是()A.B.C.D.5.(滚动交汇考查)有四个关于三角函数的命题:p1:x∈R,sin∃2+cos2=;p2:x,y∈R,sin(x-y)=sinx-siny;∃p3:x∈[0,∀π],=sinx;p4:sinx=cosyx+y=⇒.其中的假命题是()A.p1,p4B.p2,p4C.p1,p3D.p2,p36.(2013·广东高考)已知中心在原点的双曲线C的右焦点为F(3,0),离心率等2圆学子梦想铸金字品牌于,则C的方程是()A.-=1B.-=1C.-=1D.-=17.(滚动单独考查)用min{a,b}表示a,b两数中的较小值.若函数f(x)=min{|x|,|x+t|}的图象关于直线x=-对称,则t的值为()A.-2B.2C.-1D.18.“a=1”是“直线x+y=0和直线x-ay=0互相垂直”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件9.抛物线y2=4x的焦点为F,点P为抛物线上的动点,点M为其准线上的动点,当△FPM为等边三角形时,其面积为()A.2B.4C.6D.410.(滚动单独考查)已知a是函数f(x)=2x-lox的零点,若0
0C.f(x0)<0D.f(x0)的符号不能确定11.设圆锥曲线Γ的两个焦点分别为F1,F2,若曲线Γ上存在点P满足|PF1|∶|F1F2|∶|PF2|=4∶3∶2,则曲线Γ的离心率等于()3圆学子梦想铸金字品牌A.或B.或2C.或2D.或12.(2014·武威模拟)若双曲线x2-y2=a2(a>0)的左、右顶点分别为A,B,点P是第一象限内双曲线上的点.若直线PA,PB的倾斜角分别为α,β,且β=mα(m>1),那么α的值是()A.B.C.D.二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上)13.若抛物线y2=2px的焦点与双曲线x2-=1的右焦点重合,则p的值为.14.(2013·江西高考)抛物线x2=2py(p>0)的焦点为F,其准线与双曲线-=1相交于A,B两点,若△ABF为等边三角形,则p=.15.(2013·湖南高考)设F1,F2是双曲线C:-=1(a>0,b>0)的两个焦点,P是C上一点,若|PF1|+|PF2|=6a,且△PF1F2的最小内角为30°,则C的离心率为.16.(滚动交汇考查)(2014·潍坊模拟)给定两长度为1的平面向量和,它们的夹角为120°,如图所示,点C在以O为圆心的圆弧上变动,若=x+y,其中x,y∈R,则x+y的最大值是.4圆学子梦想铸金字品牌三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(10分)(滚动单独考查)(2014·滨州模拟)设△ABC的内角A,B,C的对应边分别为a,b,c,已知a=1,b=2,cosC=.(1)求△ABC的边c的长.(2)求cos(A-C)的值.18.(12分)(2014·淮南模拟)如图,椭圆C:+=1(a>b>0)的左、右焦点分别为F1,F2,上顶点为A,在x轴负半轴上有一点B,满足=,AB⊥AF2.(1)求椭圆C的离心率.(2)D是过A,B,F2三点的圆上的点,D到直线l:x-y-3=0的最大距离等于椭圆长轴的长,求椭圆C的方程.19.(12分)(滚动单独考查)设数列{an}满足:a1=5,an+1+4an=5,(n∈N*).(1)是否存在实数t,使{an+t}是等比数列?(2)设数列bn=|an|,求{bn}的前2014项和S2014.5圆学子梦想铸金字品牌20.(12分)(滚动单独考查)(2014·北京模拟)在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC的中点,又∠CAD=30°,PA=AB=4,点N在线段PB上,且=.(1)求证:BD⊥PC.(2)求证:MN∥平面PDC.(3)设平面PAB∩平面PCD=l,试问直线l是否与直线CD平行,请说明理由.21.(12分)(滚动单独考查)已知f(x)=ax-lnx,x∈(0,e],g(x)=,其中e是自然常数,a∈R.(1)讨论a=1时,f(x)的单调性、极值.(2)求证:在(1)的条件下,f(x)>g(x)+.(3)是否存在实数a,使f(x)的最小值是3,若存在...