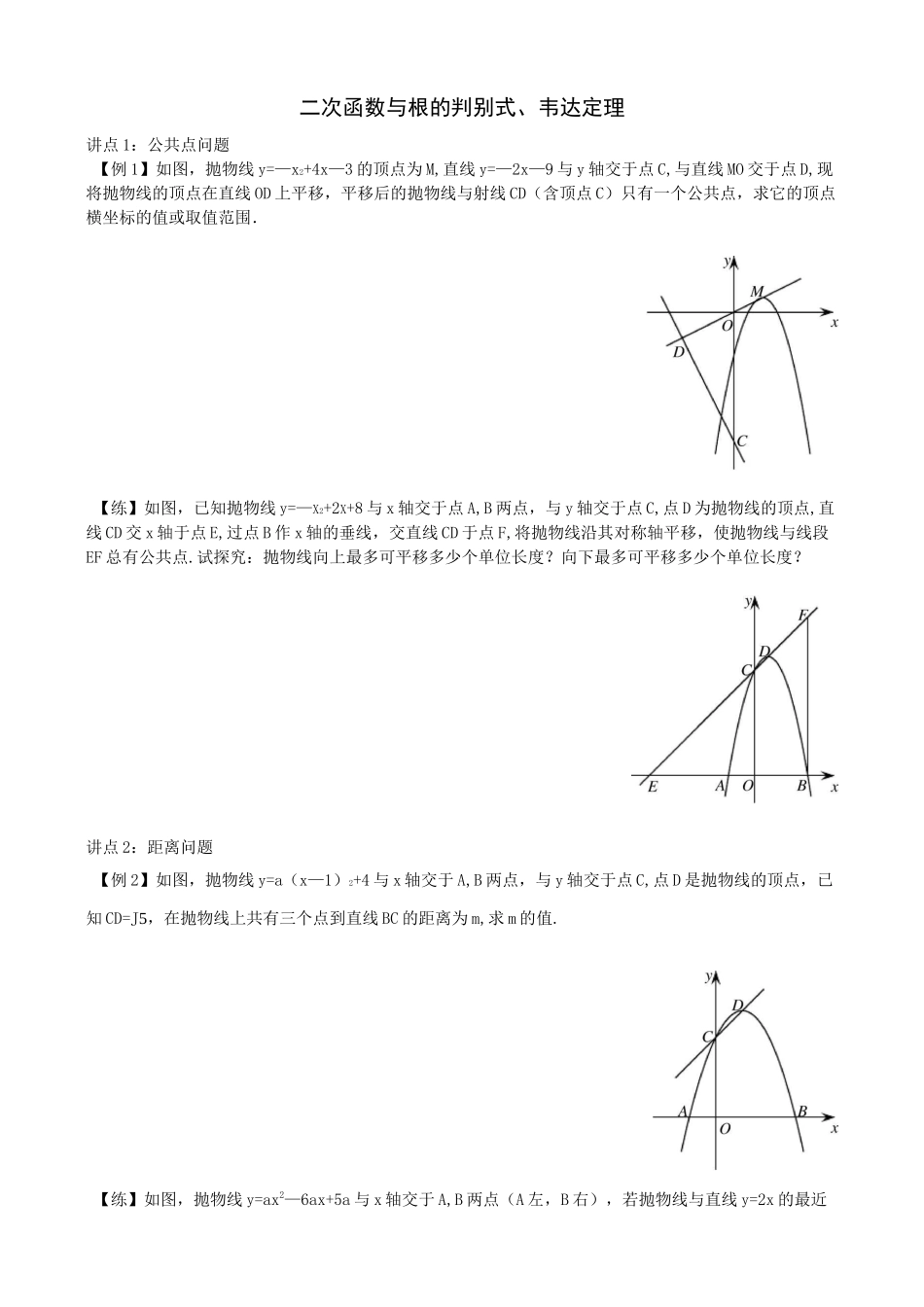
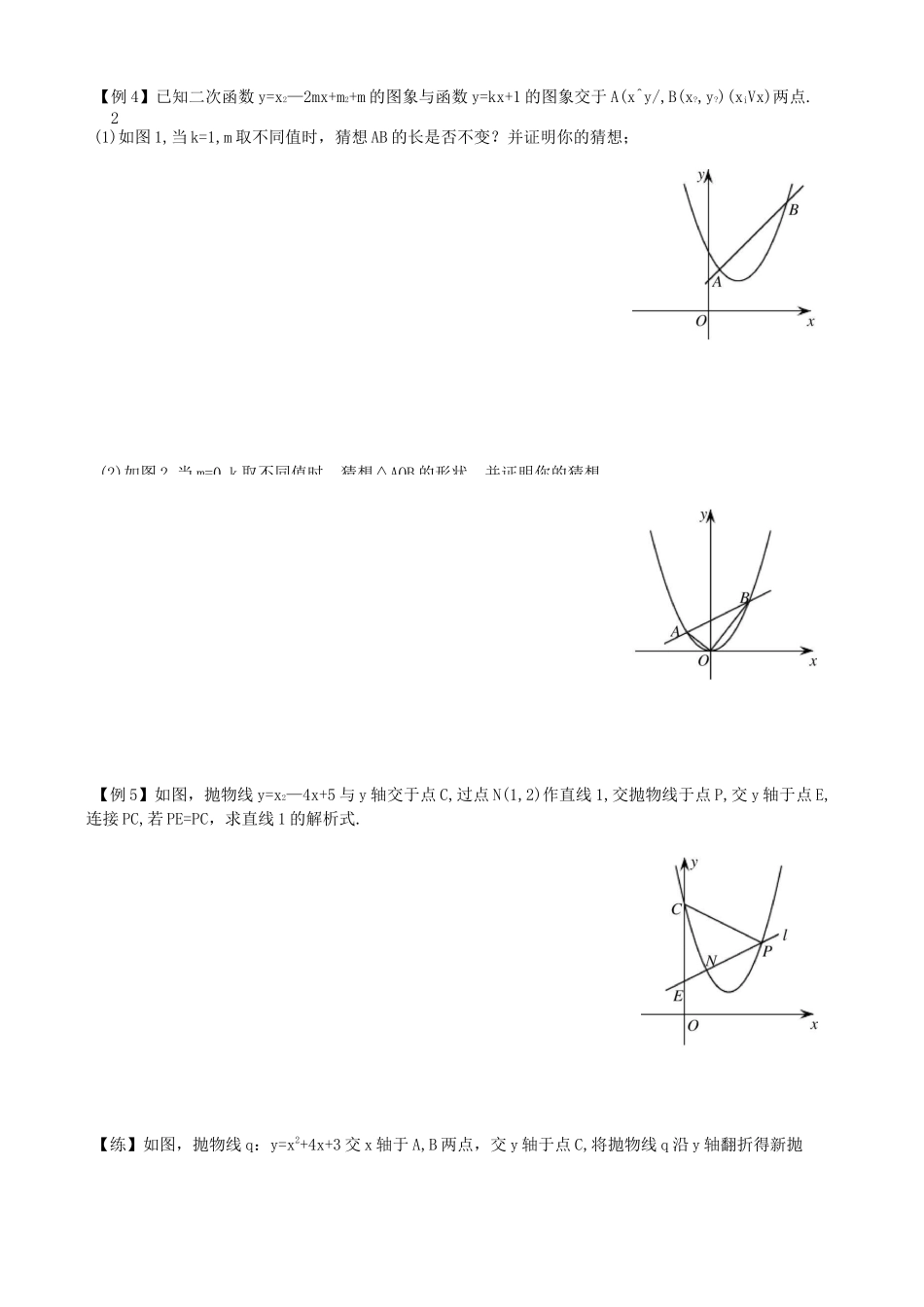
二次函数与根的判别式、韦达定理讲点1:公共点问题【例1】如图,抛物线y=—x2+4x—3的顶点为M,直线y=—2x—9与y轴交于点C,与直线MO交于点D,现将抛物线的顶点在直线OD上平移,平移后的抛物线与射线CD(含顶点C)只有一个公共点,求它的顶点横坐标的值或取值范围.【练】如图,已知抛物线y=—X2+2X+8与x轴交于点A,B两点,与y轴交于点C,点D为抛物线的顶点,直线CD交x轴于点E,过点B作x轴的垂线,交直线CD于点F,将抛物线沿其对称轴平移,使抛物线与线段EF总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?讲点2:距离问题【例2】如图,抛物线y=a(x—1)2+4与x轴交于A,B两点,与y轴交于点C,点D是抛物线的顶点,已知CD=J5,在抛物线上共有三个点到直线BC的距离为m,求m的值.【练】如图,抛物线y=ax2—6ax+5a与x轴交于A,B两点(A左,B右),若抛物线与直线y=2x的最近点之间的距离为一亍,求a的值.讲点3:隐藏判别式【例3】如图,点P是直线l:y=—2x—2上的点,过点P的另一条直线m交抛物线尸x与A,B两点,试证明:对于直线l上任意给定的一点P,在抛物线上都能找到点A,使得PA=AB成立.【练】如图,已知二次函数y=a(x2—6x+8)(a>0)的图象与x轴分别交于点A,B,与y轴交于点C,点D是抛物线的顶点.当点P在抛物线对称轴上时,设点P的纵坐标t是大于3的常数,试问:是否存在一个正数a,使得四条线段PA,PB,PC,PD与一个平行四边形的四条边对应相等(即这四条线段能构成平行四边形)?请说明理由.讲点4:交点间的距离(2)如图2,当m=0,k取不同值时,猜想△AOB的形状,并证明你的猜想.【例4】已知二次函数y=x2—2mx+m2+m的图象与函数y=kx+1的图象交于A(x^y/,B(x?,y?)(xiVx)两点.2(1)如图1,当k=1,m取不同值时,猜想AB的长是否不变?并证明你的猜想;【例5】如图,抛物线y=x2—4x+5与y轴交于点C,过点N(1,2)作直线1,交抛物线于点P,交y轴于点E,连接PC,若PE=PC,求直线1的解析式.【练】如图,抛物线q:y=x2+4x+3交x轴于A,B两点,交y轴于点C,将抛物线q沿y轴翻折得新抛物线C2,过点c作直线l交抛物线q于点M,交抛物线C2于点N,若MN=W2,求直线l的解析式.三、对称问题【例6】如图,已知抛物线y=X2—2X—3,直线y=kx—1与抛物线交于P,Q两点,且y轴平分线段PQ,求k的值.【练】如图,已知抛物线尸X—X+3,过点D(0,-2)的直线与抛物线交于点M,N,与汀由交于点E,且点M,N关于点E对称,求直线MN的解析式.四、与面积结合【例7】如图,抛物线y=X2—4X+5顶点为M,平移直线y=x交抛物线于点H,K,若=3,求平移后△MHK直线的解析式.课后反馈】1.如图,已知抛物线y=X2—2X—3与x轴交于A,B两点,与y轴交于点C,将抛物线沿对称轴向上平移k个单位长度后与线段BC交于D,E两个不同的点,求k的取值范围.2.如图,抛物线y=ax2—6ax+5a与x轴交于A,B两点(A左,B右),若抛物线不通过直线y=2x上方的点,求抛物线顶点纵坐标的取值范围.133.如图,抛物线丫=-x2+—x+2与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,将抛物42线沿直线BC平移,与射线AC(含点A)仅有一个公共点,求抛物线顶点横坐标的值或取值范围.4.如图,已知抛物线C:y=x2—2x+4和直线l:y=—2x+8,直线y=kx(k>0)与抛物线C交于A,B两点,与直线l交于点P,分别过A,B,P作x轴的垂线,垂足依次为B「P1,若1OA+丄OB1u~OP求u的值.5.如图1,抛物线q:y=x2+4X+3顶点为M,抛物线C?与抛物线q开口方向相反,形状相同,顶点为N,且M,N关于点P(0,2)对称.(1)求抛物线C的解析式;2(2)直线y=m交抛物线q于点A,B,交抛物线C?于点C,D,若AB=2CD,求m的值;