函数奇偶性教学设计的方案VIP免费

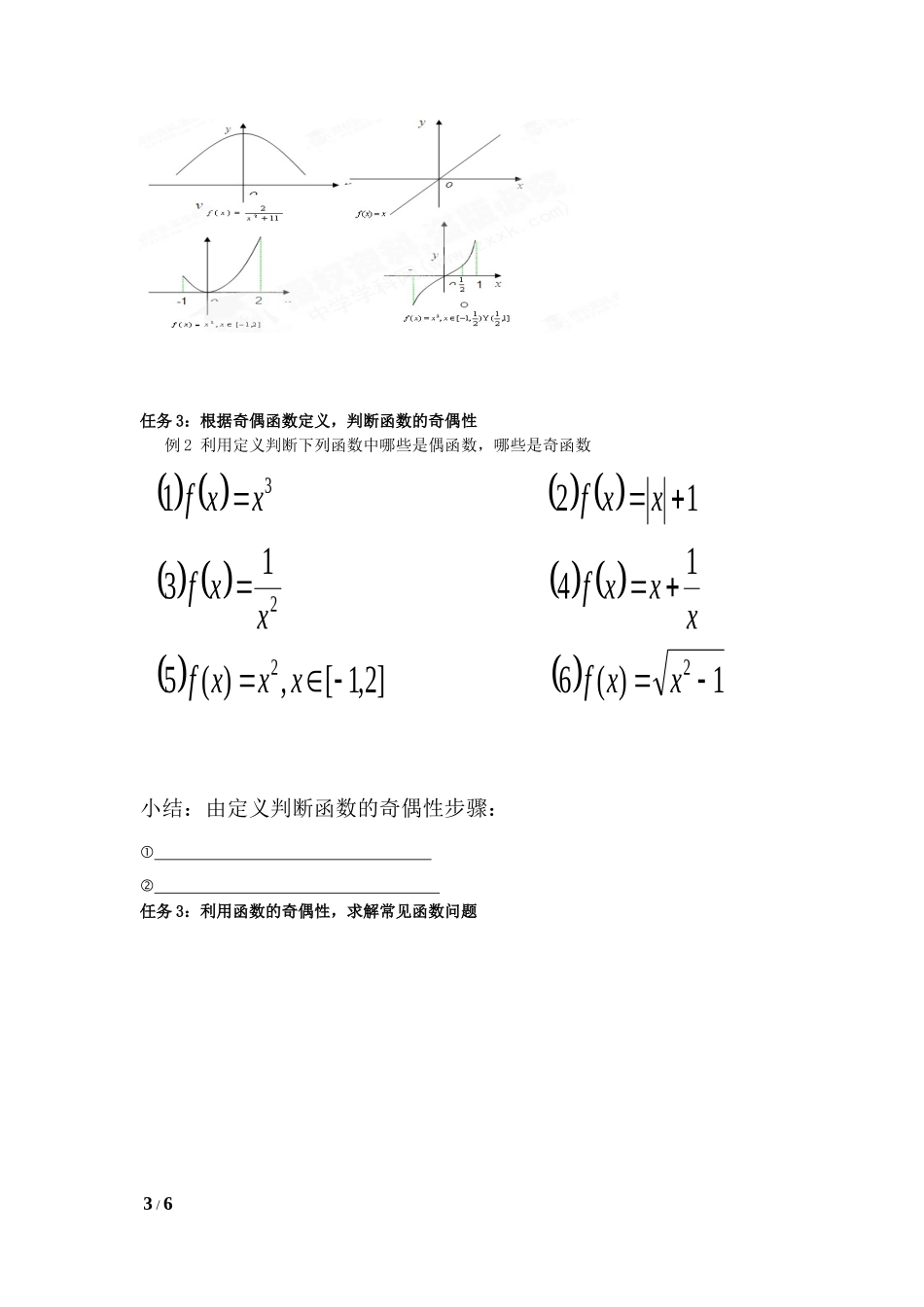
函数奇偶性教学设计的方案富源县第二中学杨立华一、教学要达到的目标1.让学生了解奇偶性的概念,会判断一些常见的函数的奇偶性，会利用函数奇偶性质处理常见函数的图像问题.重点掌握函数奇偶性的判断方法。2.在奇偶性概念形成过程中,培养学生的观察,归纳能力,同时渗透数形结合和特殊到一般的思想方法.二、教学重难点部分重点：奇偶性概念的形成与函数奇偶性的判断处理方法；难点：对概念的认识及函数奇偶性的判断方法三、教学过程1.引入新课任务1：感受奇函数和偶函数的定义(1)偶函数的定义:如果对于函数的定义域内任意一个,都有1/6,那么就叫做偶函数.(2)奇函数的定义:如果对于函数的定义域内任意一个,都有,那么就叫做奇函数.对定义的辨析理解和应用：如何判断函数奇偶性？先看定义域是否关于原点对称，如果不是关于原点对称，则函数没有奇偶性；若定义域关于原点对称，且满足f(-x)=f(x),f(x)是偶函数；满足f(-x)=-f(x),f(x)是奇函数。反之，f(x)是非奇非偶函数函数奇偶性的重要结论：(1)如果一个奇函数f(x)在原点处有定义,即f(0)有意义,那么一定有f(0)=0,有时可以用这个结论来否定一个函数为奇函数.(2)如果函数f(x)是偶函数,那么f(x)=f(-x)=f().（3）奇、偶函数在各自对称区间上的单调性如何?提示:根据奇、偶函数图象的对称性可以推知:奇函数在关于原点对称的区间上若有单调性,则其单调性完全相同;偶函数在关于原点对称的区间上若有单调性,则其单调性恰恰相反.奇函数图象关于原点对称,偶函数图象关于y轴对称.(4)函数按其是否具有奇偶性可分为四类:奇函数；偶函数；既奇又偶函数；非奇非偶函数(板书)；既是奇函数也是偶函数如：,,,,它们显然是不同的函数,但它们都是既是奇函数也是偶函数.任务2.根据下列函数图像，判断函数的奇偶性。小结：由图像判断函数的奇偶性步骤：练习：根据下列函数图象,判断函数奇偶性.2/642-2-44642-2-55-4-3-243-1122-2-4-6-8-332-2-4-6-5-32任务3：根据奇偶函数定义，判断函数的奇偶性例2利用定义判断下列函数中哪些是偶函数，哪些是奇函数小结：由定义判断函数的奇偶性步骤：任务3：利用函数的奇偶性，求解常见函数问题3/61)(6]2,1[,)(514131212223xxfxxxfxxxfxxfxxfxxf例1.已知f（x）定义在R上的偶函数，当x>0时，f（x）=x2+2x,求x<0时，f（x）的解析式。例2.设奇函数f(x)的定义域为[-5,5],若当x∈[0,5]时,f(x)的图象如图所示,求不等式f(x)<0的解集.思路分析:利用奇函数图象的对称性,画出函数f(x)在[-5,0]上的图象,再根据图象写出不等式f(x)<0的解集.解:因为函数f(x)是奇函数,所以函数f(x)在[-5,5]上的图象关于原点对称.根据f(x)在[0,5]上的图象画出在[-5,0]上的图象,如图中虚线所示.由图象知不等式f(x)<0的解集为{x|-20的x的集合是.2.已知函数y=f(x)是偶函数,且在[0,+∞)上单调递减.若f(a)0)2.判断下列函数的奇偶性3．若函数y=f(x)是奇函数，f(1)=3，则f(−1)的值为____________.4.如果奇函数f(x)在[3,7]上是增函数，且最小值是5，那么f(x)在[−7,−3]上是（）A．增函数，最小值是-5B．增函数，最大值是-5C．减函数，最小值是-5D．减函数，最大值是-56已知f(x)是定义在¿上的奇函数，当x>0时，f(x)的图象如右图所示，那么f(x)的值域是.7．已知分段函数f(x)是奇函数，当x∈[0,+∞)时的解析式为y=x2，则这个函数在区间(−∞,0)上的解析式为．5/6]3,1[,)()6(1)()5(0)()4(5)()3(1)()2(1)()1(22xxxfxxfxfxfxxfxxxf322xyO8.已知偶函数f(x)定义在R上,且当x≥0时,f(x)=x2-2x,求f(x)的解析式.9.已知f(x)定义在R上,且对任意实数x,y,恒有f(x+y)=f(x)+f(y).(1)求f(0);(2)求证:f(x)是奇函数;(3)若f(x)在(0,+∞)上是增函数,证明f(x)在(-∞,0)也是增函数.6/6