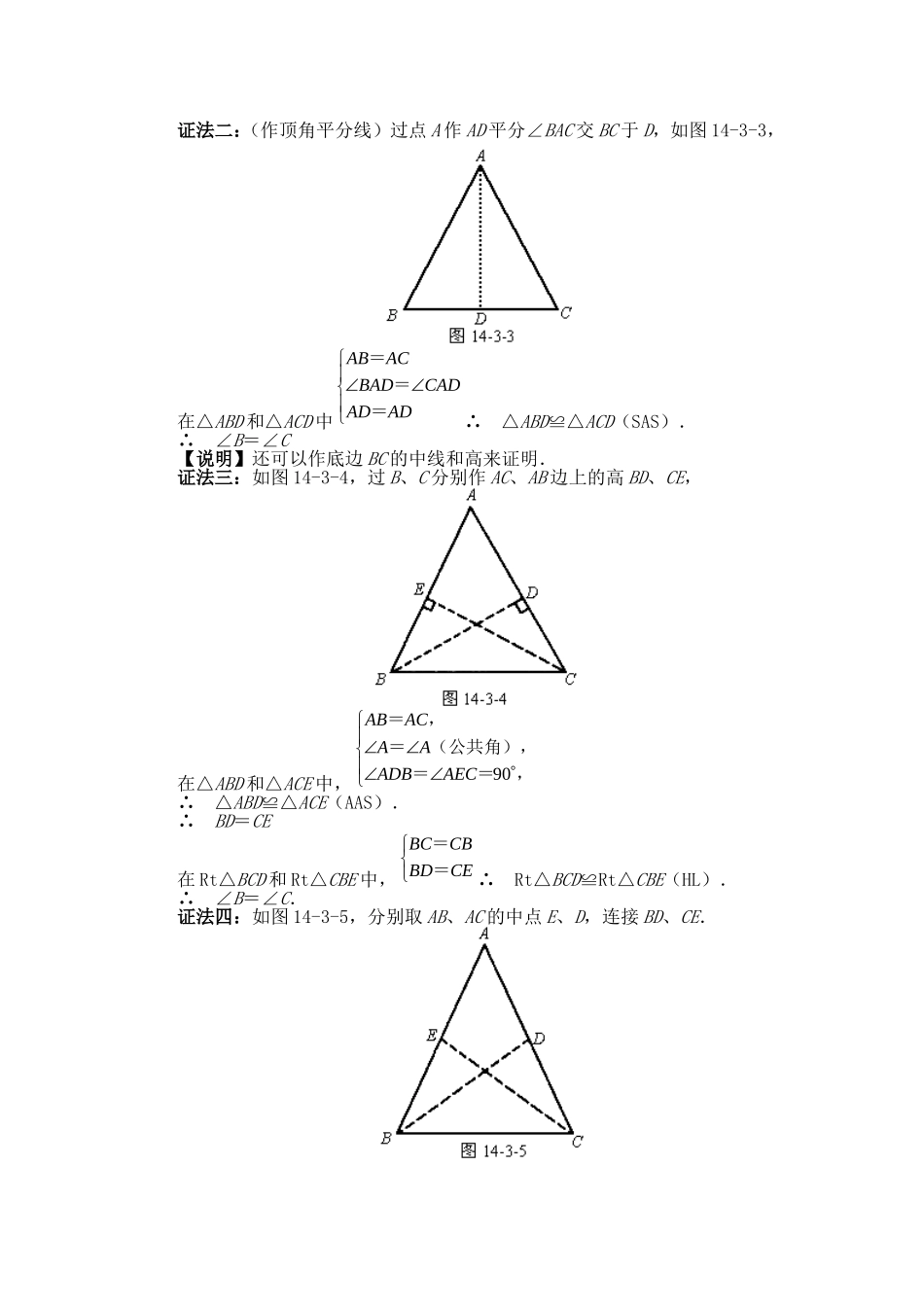
等腰三角形·要点全析1.等腰三角形(isoscelestriangle)有两条边相等的三角形叫做等腰三角形.如图14-3-1,△ABC中,AB=AC,则△ABC是等腰三角形.相等的两条边叫腰,另一条边BC叫底边,两腰所夹的角叫顶角,如∠BAC,底边和腰的夹角∠ABC和∠ACB叫底角.如图14-3-2中,∠C=90°,AC=BC,那么,AC、BC为腰,AB边为底,∠A、∠B为底角,∠C为顶角.【说明】要理解等腰三角形的定义,需注意以下几点:(1)等腰三角形的底不一定在下方,而顶角不一定在上方,如图14-3-2中,AB为底,∠C为顶角.它是根据两腰的位置来确定的.(2)等腰三角形的三边仍要满足条件:任意两边之和大于第三边(或任意两边之差小于第三边).若图14-3-1中,AB=AC=m,BC=a,则2m>a,即m>2a时,才能构成三角形,否则不成立.如边长分别为2,2.5的三条线段不能构成三角形因为2+2<5.例如:(1)下列各组数据为边长时,能否组成三角形?①a=2,b=3,c=5;②a=4,b=3,c=2;③a=1,b=2,c=2;④a=2005,b=2004,c=2008.(2)已知等腰三角形的两边为6cm,7cm,求其周长.(3)已知等腰三角形的两边长为2cm,7cm,求其周长.解:(1)①由于2+3=5,即a+b=c,而不满足a+b>c,∴不能组成三角形.②由于2+3=5>4,即b+c>a,所以a、b、c可以组成三角形.③由于1+2>2,即a+b>c,所以a、b、c可以组成三角形.④由于a+b>c,因此a、b、c可以组成三角形.(2)因等腰三角形的两边长分别为6cm、7cm当腰长为6cm时,周长为6+6+7=19(cm)当腰长为7cm时,周长为6+7+7=20(cm).∴等腰三角形的周长为19cm或20cm.(3)因等腰三角形的两边长分别为2cm,7cm,所以腰长为7cm,而不能是2cm.若为2cm,则2+2=4<7,不能组成三角形.因此周长为7+7+2=16(cm),∴等腰三角形的周长为16cm.2.等腰三角形的性质1等腰三角形的两个底角相等(简写成“等边对等角”)如图14-3-3,△ABC中,AB=AC,则∠B=∠C证法一:(利用轴对称)过点A作△ABC的对称轴AD. AB=AC,∴点A在BC的垂直平分线上.又 AD为△ABC的对称轴,∴△ABD≌△ACD(轴对称性质).∴∠B=∠C证法二:(作顶角平分线)过点A作AD平分∠BAC交BC于D,如图14-3-3,在△ABD和△ACD中ADADCADBADACAB===∴△ABD≌△ACD(SAS).∴∠B=∠C【说明】还可以作底边BC的中线和高来证明.证法三:如图14-3-4,过B、C分别作AC、AB边上的高BD、CE,在△ABD和△ACE中,,==(公共角),=,=90AECADBAAACAB∴△ABD≌△ACE(AAS).∴BD=CE在Rt△BCD和Rt△CBE中,CEBDCBBC==∴Rt△BCD≌Rt△CBE(HL).∴∠B=∠C.证法四:如图14-3-5,分别取AB、AC的中点E、D,连接BD、CE. AB=AC,AD=DC=21AC,AE=BE=21AB,∴AD=BE=AE=DC在△ABD和△ACE中,,=,=,=AEADAAACAB∴△ABD≌△ACE(SAS).∴BD=CE.在△BCE和△CBD中,=,=,=CDBEBDCECBBC∴△BCE≌△CBD(SSS).∴∠ABC=∠ACB.【说明】从以上的证法二、三、四中可以看出,要证两角相等,都是想方设法把它们放在两个三角形中,证两个三角形全等.3.等腰三角形的性质2(简称“三线合一”)等腰三角形的顶角平分线、底边上的中线、底边上的高线相互重合.如图14-3-6,在△ABC中,AB=AC,AD为顶角的平分线,那么AD既是中线,又是高线,这三条线重合.在使用时,在这三条线段中,只要作出其中一条,另外两条也就可以认为作出来了.即△ABC中,AB=AC,若AD平分∠BAC,则AD⊥BC,BD=CD;若BD=CD,则AD⊥BC,∠BAD=∠CAD;若AD⊥BC,则BD=DC,∠BAD=∠CAD.因此,等腰三角形中的这条线非常重要,一旦作出,边、角的等量关系就都有了.【说明】(1)“三线合一”仅限于等腰三角形中才有,其他三角形中没有.(2)在一般三角形中,这三条线是不会重合的.如图14-3-7,在△ABC中,AD为高,AE为中线,AF平分∠BAC,因此,这三条线不重合.只有等腰时,三条线才会重合;反过来,若某一三角形中三线重合,则该三角形为等腰三角形.(3)在今后的证明题中,经常会使用“三线合一”进行证明....