三垂线定理课件VIP免费

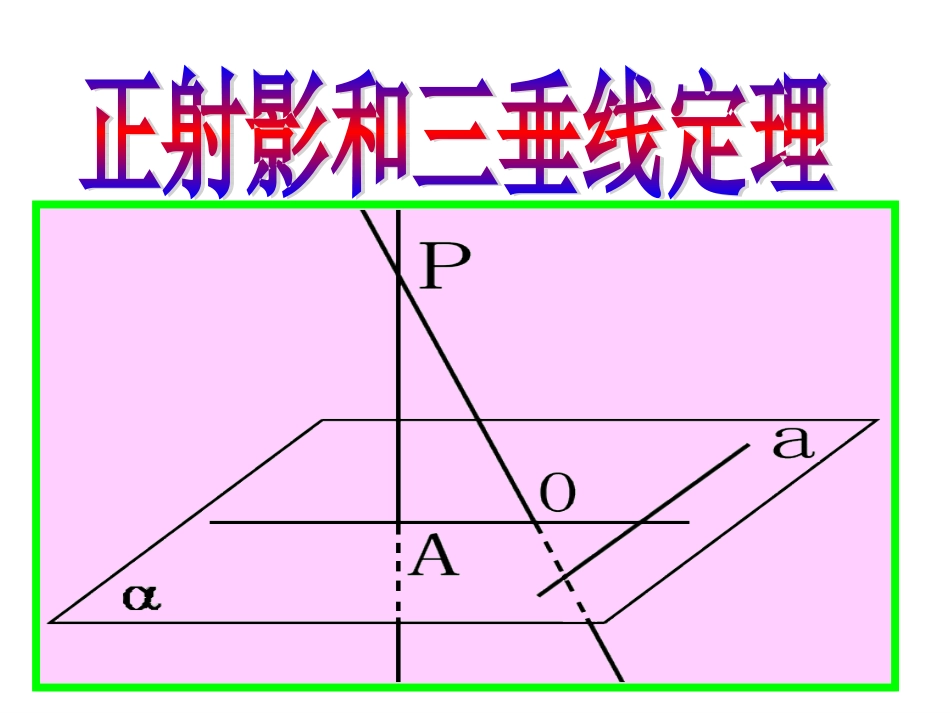
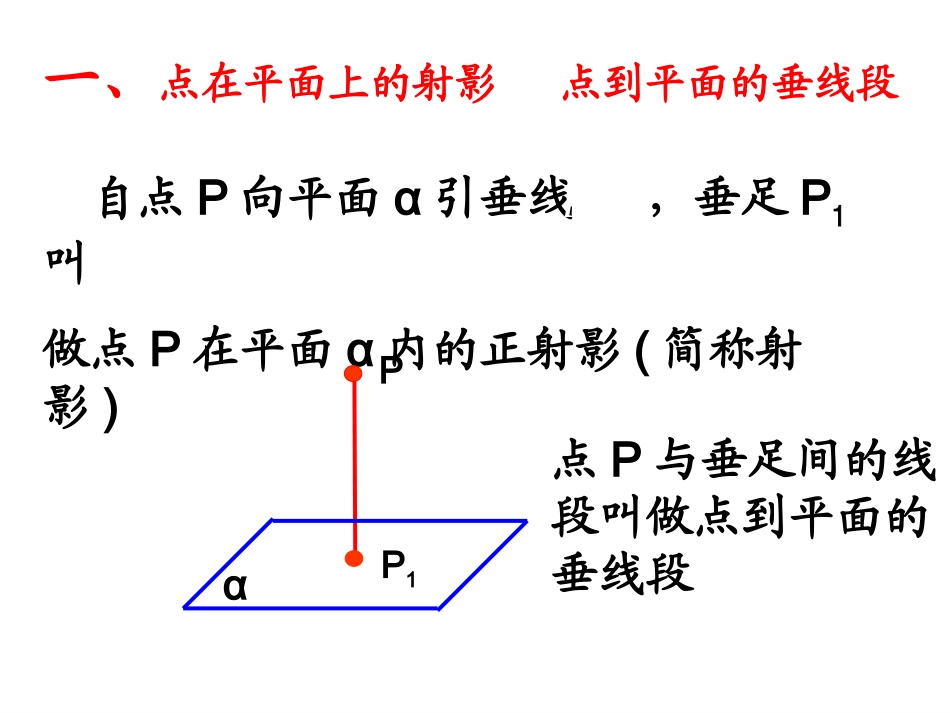
复习回顾:1、直线与平面垂直的定义，判定定理，性质定理。2、如何定义直线外一点在直线上的射影？一、点在平面上的射影点到平面的垂线段P1l自点P向平面α引垂线，垂足P1叫做点P在平面α内的正射影(简称射影)lPα点P与垂足间的线段叫做点到平面的垂线段如果图形F上的所有点在一平面内的射影构成的图形,则叫做图形F在这个平面上的射影.FF二、图形在平面内的射影FF'FOAPOPO于如果一条直线和一个平面相交，但不和这个平面垂直，那么这条直线叫做平面的斜线．斜线上一点与斜足间的线段叫做斜线段(线段AP)．斜线和平面的交点叫做斜足A．斜线PA在平面的射影为直线OA两条平行线;或一条直线练习１、1、直线l⊥α于Ａ点,则l在α内的射影为2、直立的⊿ABC在水平面α内的射影为4、空间中两条平行直线a,b在同一平面内的射影可能是3、空间中一条直线在一个平面内的射影可能是点Ａ线段一个点两个点;一条直线一个点和一条直线;两条相交直线;一个点和一条直线;5、空间中两条相交直线a,b在同一平面内的射影可能是两条相交直线;一条直线6、空间中两条异面直线a,b在同一平面内的射影可能是7、空间中两条直线a,b在同一平面内的射影可能是两条平行线;两条平行线;两条相交直线;两个点;一条直线ACBDE⑴垂线段比任何一条斜线段都短从平面外一点向这个平面所引的垂线段和斜线段AB、AC、AD、AE…中,哪一条最短？(简称:垂线段最短)ACBOOB=OCAB=ACOB＞OCAB＞ACAB=ACOB=OCAB＞ACOB＞OC（2）射影相等的两条斜线段相等,射影较长的斜线段也较长（3）相等的斜线段的射影相等,较长的斜线段的射影也较长从平面外一点向这个平面所引的垂线段和斜线段及其它们在该平面内的射影：从平面外从平面外一点向这个平面所引的垂线段和斜线段中.(1)射影相等的两条斜线段相等,射影较长的斜线段也较长(2)相等的斜线段的射影相等,较长的斜线段的射影也较长(3)垂线段最短一、射影定理ACBOAPO、PA分别是平面的垂线、斜线,OA是PA在平面上的射影.已知在平面内的一条直线,若它和这个平面的一条斜线的射影垂直,则它也和这条斜线垂直二、三垂线定理二、三垂线定理求证：a⊥PA１、三垂线定理１、三垂线定理a,a⊥OA。OaAP已知PO、PA分别是平面的垂线、斜线,OA是PA在平面上的射影.a⊥OAa⊥PA∵OA⊥aOAOPO∵PA平面PAO∴a⊥PA∴PO⊥a∴a⊥平面PAO∵PO⊥a证明：a,求证：OaAPOaAP在平面内的一条直线,若它和这个平面的一条斜线的射影垂直,则它也和这条斜线垂直二、三垂线定理二、三垂线定理１、１、三垂线定理三垂线定理在平面内的一条直线,若和这个平面的一条斜线垂直,则它也和这条斜线的射影垂直２、三垂线定理的逆定理,逆定理OaAP二、三垂线定理，二、三垂线定理，逆定理１、三垂：aPAaOAPO,,２、时，POPAaOAa三垂线定理三垂线定理三垂线的三垂线的逆定理⊥直线射影⊥直线斜线即：三垂线定理三垂线定理三垂线的三垂线的逆定理练习(3)若P到△ABC三边AB,BC,CA的距离相等，则O为△ABC的心(2)若PA⊥BC,PB⊥AC,则O为△ABC的心(1)若PA=PB=PC,则O为△ABC的心外垂内PCBAO例１、四面体ABCD中,若AB⊥CD,BC⊥AD求证：AC⊥BDOADCB作AO⊥平面BCD于点O,连接BO,CO,DO.则BO,CO,DO分别为AB,AC.AD在平面BCD上的射影。∵ABCDBOCD⊥∴⊥证明:同理COBD⊥，于是O是△BCD的垂心，∴DOBC,⊥于是ADBC.⊥OABCPOABC平面OPABC练习2、已知：点是的垂心，，垂足为求证：DABCPO例2、若一个角所在平面外一点到角的两边距离相等,则这一点在平面上的射影在这个角的平分线上已知：∠BAC在平面内,点P,PE⊥AB,PF⊥AC,PO⊥,垂足分别是E、F、O,PE=PF.分析:要证∠BAO=∠CAOPCBAOF求证:∠BAO=∠CAO只须证OE=OF,OE⊥AB,OF⊥ACE练习3.已知点O是△ABC的BC边上的高上的任意一点，且OP⊥平面ABC,求证PABC⊥ABCDPO证明：∵OP⊥平面ABCAO是PA在平面ABC内的射影，又∵AOBC⊥，∴PABC⊥。（三垂线定理）练习4.如图,PD⊥平面ABC,AC=BC,D为AB的中点，求证ABPC⊥ABCDP证明：∵AC=BC，D是BC的中点，∴ABCD⊥，∵PD⊥平面ABC，∴CD是PC在平面ABC内的射影，∴ABPC⊥（三垂线定理）练习5.如图:ABCD是矩形,PA⊥平面AC，连结PB,PC,PD，指出图中有哪些三角形是直角三角形，并说明理由PABCD解:PA平面AC,PAAB,PAAD.PAB,PAD.都是直角三形又ABBC,BC,PBPBC.是直角三角形,PDC.同理也是直角三角形