人教版八年级下册181勾股定理4（共15张PPT）VIP免费

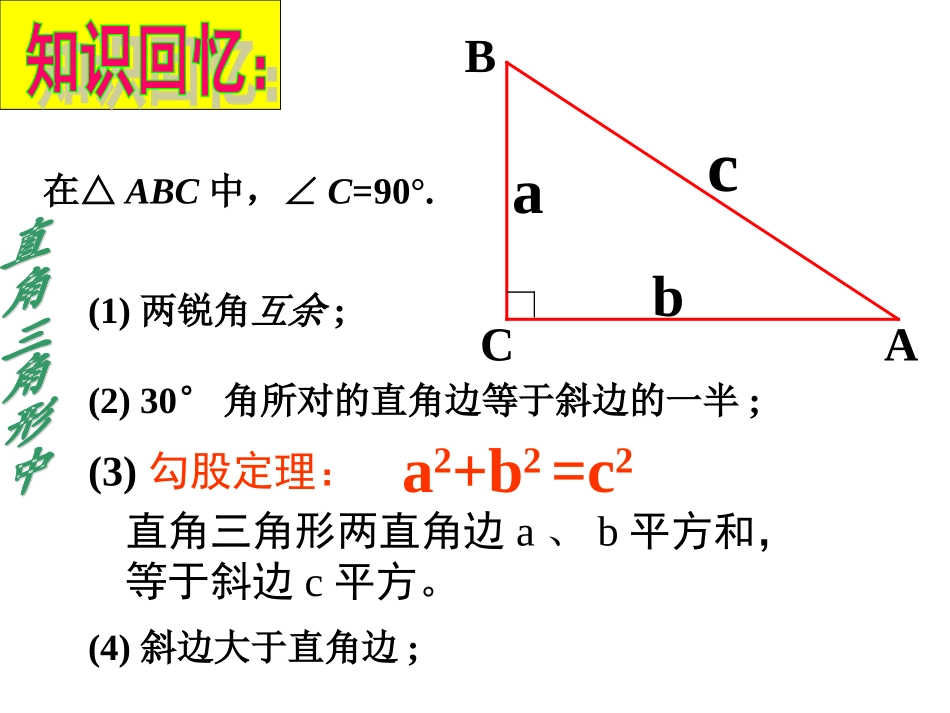
SA+SB=SCa2+b2=c2abcSASBSCcab在△ABC中，∠C=90°.(4)斜边大于直角边;(1)两锐角互余;(2)30°角所对的直角边等于斜边的一半;CAB(3)勾股定理：a2+b2=c2直角三角形两直角边a、b平方和，等于斜边c平方。(2)可用勾股定理建立方程.(2)若a=２，c=３，则b=__________；(3)若c=13，b=5，则a=__________；(4)若a:b=3:4,c=10,则a=______,b=_______.(1)若a=3，ｂ=4，则c=__________；在Rt△ABC中，∠Ｃ=90°.abcＡＣＢ小结(1)在直角三角形中,已知两边,可求第三边;512568方程思想1、已知：Rt△ＡBC中，AB＝４，AC＝３,则BC的长为.5或743ACB43CAB分类讨论2.三角形ABC中,AB=10,AC=17,BC边上的高线AD=8,求BC∟D∟DABCABC1017817108分类讨论1.小溪边长着两棵树，恰好隔岸相望，一棵树高30尺，另外一棵树高20尺；两棵树干间的距离是50尺，每棵树上都停着一只鸟，忽然两只鸟同时看到两树间水面上游出一条鱼，它们立刻以同样的速度飞去抓鱼，结果同时到达目标。问这条鱼出现在两树之间的何处？3020x50-x22223020(50)xx20()x解得尺方程思想小明想知道学校旗杆的高，他发现旗杆顶端的绳子垂到地面还多1米，当他把绳子的下端拉开5米后，发现下端刚好接触地面，求旗杆的高度。x+1x52225(1)xx222521xxx2251x12x1练习&&11☞☞方程思想2.在△ABC中，AB=15，BC=14，AC=13，求(1)ABC△的面积；(2)求腰AC上的高ABC151413Dx14-x22221513(14)xx22221513(14)xx28214(214)x9x解得222215912ADABBD1212ABCSBCAD11412842E方程思想面积法1.在ABC中,∠C=90°,AC=6,CB=8,则ABC面积为_____,斜边为上的高为______.244.8AABBCCDD练习&&22☞☞面积法2.已知:一个三角ABC,AB=AC=13,BC=10,(1)求它的面积；(2)求腰AC上的高.ABC13135512DE12ABCSBCAD110126021602ABCSACBE13120BE12013BE(1)如图，在四边形ABCD中，∠BAD=900，∠DBC=900，AD=3，AB=4，BC=12，求CD的长和四边形ABCD的面积。练习&&33☞☞(3)已知：c＝10，a＝6，求正三角形的面积.(2)已知：c＝13，a＝5，求阴影部分面积accab34512136305131221121822S6108484316318DABC如图，∠ACB=∠ABD=90°，CA=CB，∠DAB=30°，AD=8，求AC的长。解：∵∠ABD=90°，∠DAB=30°∴BD=AD=421在Rt△ABD中,根据勾股定理484822222BDADAB在Rt△ABC中，CBCACBCAAB且,222242122222ABCACAAB62AC又AD=8ABCD30°84xx222284xx2248x224x24x取正数得4626如图，∠C=90°，图中有阴影的三个半圆的面积有什么关系？ACBS3S1S2直角三角形ABC的面积为20cm2,在AB的同侧分别以AB、BC、CA为直径做三个半圆，求阴影部分的面积。ACB二、方法一、知识点善于把实际问题转化为我们熟悉的数学问题三、数学思想化归思想1.勾股定理：直角三角形中两直角边的平方和等于斜边的平方.即a²+b²=c²2.勾股定理不仅仅是直角三角形三边的数量关系,还是一种面积关系.3.勾股定理的应用.你能谈谈学习这节内容的收获和体会吗？