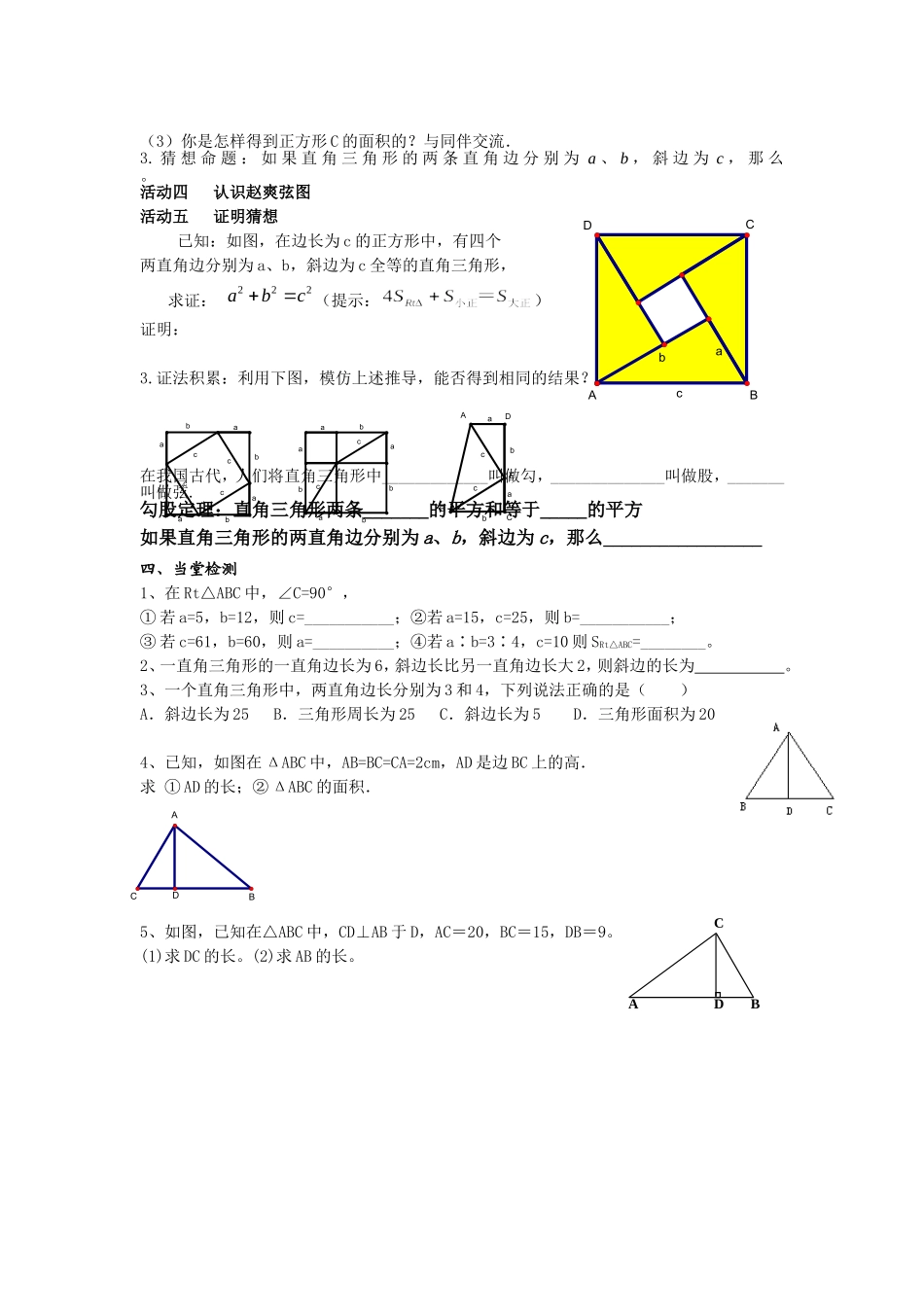
勾股定理导学案第一课时学习目标:1.经历勾股定理的探索过程,能熟记定理的内容.2.能运用勾股定理由直角三角形的已知两边求第三边.3.能运用勾股定理解一些简单的实际问题.重点:勾股定理的探索和应用.难点:勾股定理的探索.学习过程:一、知识回顾(用学过的知识完成下列填空)①含有一个的三角形叫做直角三角形.②已知Rt△ABC中的两条直角边长分别为a、b,则S△ABC=.③已知梯形上下两底分别为a和b,高为(a+b),则该梯形的面积为.④完全平方公式:(a±b)2=.⑤在Rt△ABC中,已知∠A=30°,∠C=90°,直角边BC=1,则斜边AB=.二、自学交流活动一动手做一做1、在右边空白处画出Rt△ABC令∠C=90°,直角边AC=3cm,BC=4cm,(1)用刻度尺量出斜边AB=________(2)计算:2、探究:之间的关系:________________活动二毕达哥拉斯的发现1、图中两个小正方形分别为A、B,大正方形为C,则三个正方形面积之间的关系:_______________2、设三个正方形围成的等腰直角三角形的直角边为a,斜边为c,则图中等腰直角三角形三边长度之间的关系:_____________________3.(1)能发现各图中三个正方形的面积之间有何关系吗?结论1:(2)观察右边两幅图,填表。A的面积B的面积C的面积左图右图1B30°□ACABCCBACABDcbaDCAB四、当堂检测1、在Rt△ABC中,∠C=90°,①若a=5,b=12,则c=___________;②若a=15,c=25,则b=___________;③若c=61,b=60,则a=__________;④若a∶b=3∶4,c=10则SRt△ABC=________。2、一直角三角形的一直角边长为6,斜边长比另一直角边长大2,则斜边的长为。3、一个直角三角形中,两直角边长分别为3和4,下列说法正确的是()A.斜边长为25B.三角形周长为25C.斜边长为5D.三角形面积为204、已知,如图在ΔABC中,AB=BC=CA=2cm,AD是边BC上的高.求①AD的长;②ΔABC的面积.5、如图,已知在△ABC中,CD⊥AB于D,AC=20,BC=15,DB=9。(1)求DC的长。(2)求AB的长。(3)你是怎样得到正方形C的面积的?与同伴交流.3.猜想命题:如果直角三角形的两条直角边分别为a、b,斜边为c,那么。活动四认识赵爽弦图活动五证明猜想已知:如图,在边长为c的正方形中,有四个两直角边分别为a、b,斜边为c全等的直角三角形,求证:222abc(提示:)证明:3.证法积累:利用下图,模仿上述推导,能否得到相同的结果?在我国古代,人们将直角三角形中_____________叫做勾,______________叫做股,_______叫做弦.勾股定理:直角三角形两条_______的平方和等于_____的平方如果直角三角形的两直角边分别为a、b,斜边为c,那么_________________bbbbccccaaaabbbbaaccaabccaabDCAEBbbbbccccaaaabbbbaaccaaACBD