整式乘法及因式分解VIP免费

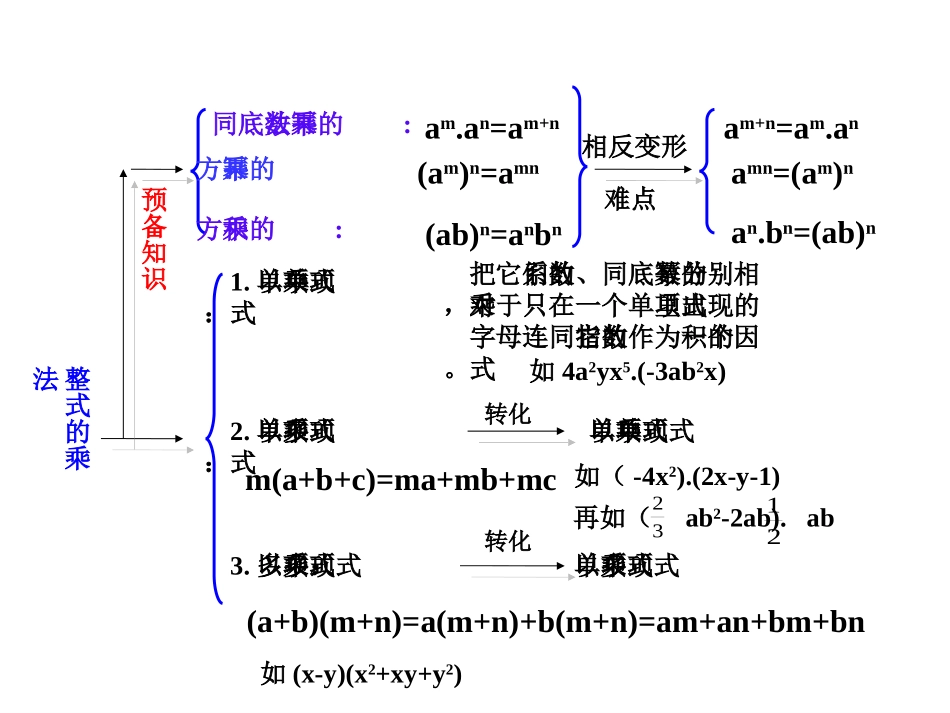
高青金钥匙培训学校成功整式的乘法同底数幂的乘法:am.an=am+n幂的乘方：(am)n=amn积的乘方:(ab)n=anbn预备知识1.单项式乘以单项式：把它们的系数、同底数的幂分别相乘，对于只在一个单项式里出现的字母连同它的指数作为积的一个因式。如4a2yx5.(-3ab2x)2.单项式乘以多项式：转化单项式乘以单项式m(a+b+c)=ma+mb+mc再如（ab2-2ab).ab3221如（-4x2).(2x-y-1)3.多项式乘以多项式：转化单项式乘以多项式(a+b)(m+n)=a(m+n)+b(m+n)=am+an+bm+bn如(x-y)(x2+xy+y2)相反变形难点am+n=am.anamn=(am)nan.bn=(ab)n想一想a2a3a5+=(1)a2aa2·=(2)(x-y)2(y-x)5=(x-y)7(8)x2()3=x5(4)··47(6)(-5)(-5)=511(-3)2·33=(-3)5(7)2(5)35a·2a=10a6(3)a3a3=2a3练习一1.计算(1)100.10m+1.10m-2(2)an+2.an+1.an.a2(3)(102)3(4)(xy3n)2+(xy6)n(5)-p.(-p)4(6)(b+2)2(b+2)5(b+2)(7)(a-2b)3(b-2a)4(8)(-a2.(-a4b3)2)3(9)(x-2y)2(y-2x)3注意：通过以上练习可知，公式中的a既可以是一个数也可以是一个字母，也可以是一个代数式。2.(1).-x2y2.xyz(2)(a2+ab-0.6b2).(-a2b2)(3)(2x+y)(x-3y)(4)3y(y2+4y+4)-y(y-3)(3y+4)(5)(2m-3n)(3m-4n)(6)若ab2=-1,则-ab(a2b5-ab3-b)的值是多少？43322334比一比算计(1)3x2()3-7x3[]x3-x4x2+1()a2()-2b2a+2b()-2ab(a-b)(2)先化简，再求值:其中a=1,b=21.公式的逆向使用公式的逆向使用nmnmaaamnnmmnaaabababa323210102101710410）（）（，求下列各式的值＝，＝已知（3）已知2m=3，2n=5，求23m+2n+2的值.1、若10x=5,10y=4,求102x+3y+1的值.2、计算：0.251000×（-2）20016701004)271()9.(3注意点：（1）指数：相加底数相乘转化（2）指数：乘法幂的乘方转化（3）底数：不同底数同底数转化（3）（1）0．12516·(－8)17；（2）逆用公式即baabnnn）（）（abbannn5050505050931244331515)2(125.0公式的反向使用公式的反向使用试用简便方法计算试用简便方法计算::((abab))nn==aann··bbnn（（mm,,nn都是正整数都是正整数））反向使用反向使用::aann··bbnn==((abab))nn(1)(1)2233××5533;;(2)(2)((-5)5)1616××((-2)2)1515(3)(3)2244××4444××((-0.125)0.125)44;;整式的乘法1.单项式乘以单项式2.单项式乘以多项式3.多项式乘以多项式逆运算预备知识am÷an=am-n当m=n时，规定：a0=1(a≠0)整式的除法1.单项式除以单项式2.多项式除以单项式3.多项式除以多项式单项式相除，把系数与同底数的幂分别相除作为商的因式，对于只在被除式里含有的字母连同它的指数作为商的一个因式。如20x4y2z÷(-x3y2)(-2a2b3c)2÷a3b241单÷单转化(a+b)÷m=a÷m+b÷m如(0.25a2b-0.5a3b2-a4b3)÷(-0.5a2b)41初中阶段不学习am.an=am+n(am)n=amn(ab)n=anbn特例乘法公式1.平方差公式2.完全平方公式(a+b)(a-b)=a2-b2(a+b)2=a2+2ab+b2(a-b)2=a2-2ab+b2相反变形因式分解(1)(-a)8÷(-a2)(2)-5a5b3c÷5a4b3(4)-3a2x4y3÷(-axy2)(5)(4×109)÷(-2×103)=-a6=-ac=3ax3y=-2×106(3)6m2n÷(-2mn)=-3m(1)(-2a4b3c)3÷(-8a4b5c)(3)(-3.6×1010)÷(-2×102)2÷(3×102)2=a8b4c2=–10(2)(6x2y3)2÷(3xy2)2=4x2y22234)21()212)(4(xxxx练习1.计算(1).x15÷÷x6(2).(-xy)x6(2).(-xy)1010÷÷(-xy)8(3)a(-xy)8(3)a2m+42m+4÷÷aam-2m-2(4).(x-2y)(4).(x-2y)44÷÷(2y-x)(2y-x)33(5).(-a)(5).(-a)55÷÷aa332.计算(1).-3a7b4c÷÷9a9a44bb22(2)28x(2)28x44yy22÷÷7x7x33y(3)4ay(3)4a3m+13m+1÷÷(-8a(-8a2m-12m-1))(4).8(m+n)(4).8(m+n)55÷÷(-(m+n)(-(m+n)33)(5).(8a)(5).(8a22+ab+a)+ab+a)÷÷aa(6).(6).已知一个多项式除以多项式已知一个多项式除以多项式aa22+4a-3+4a-3所得的商式是所得的商式是2a+1,2a+1,余式余式是是2a+8,2a+8,求这个多项式。求这个多项式。•计算（一）：•（1）（2x＋3）（2x－3）•（2）（－x＋2）（－x－2）•（3）（－2x＋y）（2x＋y）•（4）（y－x）（－x－y）•(5)1998×2002填空(1).(a+)2=a2+6a+。(2).(2x-)2=4x2-+25(3).a2+b2=(a-b)2+。(4).(x-y)2+=(x+y)2想一想下列计算是否正确？如不正确，应如何改正？(-x+6)(-x-6)=-x2-6(1)2-x-...